As you prepare for your Unit 1 and 2 Maths Methods SACs, you will undoubtedly be wanting to look for and complete practice SACs.
Here, we’ll go through what you can expect in these practice SACs, along with fully worked examples. We’ll also give you tips on how to translate these practice SACs into success in your real SAC!
Let’s dive in!
Practice SACs VS Real SACs
CAS-Free Short Answer
Multiple Choice
Application Questions
Answers
Practice SACs VS Real SACs — What’s the difference?
Luckily, most practice SACs will end up being very close to your real SAC! Some things that you’ll want to consider are:
- What is the content being covered? If your SAC is just covering quadratic equations, make sure you don’t go looking for questions about trigonometry!
- What type of questions will you be asked? Depending on the specific SAC you will sit, you could be asked many different styles of questions. This is important so that you are finessing the right skills
When you’re completing practice SACs, you should also keep these principles in mind:
- Use practice SACs as practice SACs! Try completing them under timed conditions, and note any particular requirements for each SAC
- Don’t fall for the trap: Your real SAC won’t mimic exactly the practice SAC. While the style of questions may be similar, the exact questions being asked will be different.
Tip: Make a note of any textbook exercises which have not appeared in your practice SACs, and spend a bit of time revising these exercises specifically.
Let’s go through what exactly are the types of questions you might see in your practice SACs.
CAS-Free Short Answer
There are certain SACs where you will not be allowed to use any notes or calculators.
The questions in these SACs are usually simpler compared to questions where calculators and notes are allowed. However, not having notes can make these questions rather tough!
Here are our tips for preparing for CAS free questions:
- Even when you’re just starting, try these questions without notes and the calculator. If you’re really stuck, then use notes and a calculator. Record which questions you use notes for!
- A common challenge is arithmetic errors. Try and develop good habits early on (e.g. checking each arithmetic calculation straight after you do them).
- You may want to use the space on the side of the paper to write out arithmetic calculations
- When you’re beginning, getting the answer correct is more important than speed. Do try and pick up the pace as you practice more, but ensure you’re still getting the right answer!
- Do not simplify or manipulate expressions/equations unless either asked, or if you think it will help. An unsimplified answer is usually still correct.
- A classic mistake is trying to simplify a final answer, but simplifying it incorrectly and losing marks!
- Create a list of “key things to remember” in relation to each concept. For example, if 𝑥 = a2, then remember that x = ± a
Specifically for graphing questions:
- Make sure to only graph and label what you are required to do.
- For every graph that you learn, make a note of what the key features are, and how to find them if necessary.
- These usually are turning points, asymptotes, axial intercepts
- Also make a note of how to recognise what general shape a graph will be from its equation!
Sometimes, these questions closely resemble textbook questions. This means that doing extra textbook questions can be a good way to consolidate specific concepts. However, the harder CAS free questions usually do not match any textbook questions – this is why you need to have strong conceptual understandings!
Did you know you can do different VCE subjects for Units 3 and 4 from Units 1 and 2s? Check out our guide to selecting VCE Subjects!
Question 1
a. Show that (𝑥 – 2) is a factor of 𝑥3 + 2𝑥2 – 4𝑥-8.
1 mark
b. Hence, find all solutions for 𝑥3 + 2𝑥2 – 4𝑥-8 = 0
3 marks
Question 2
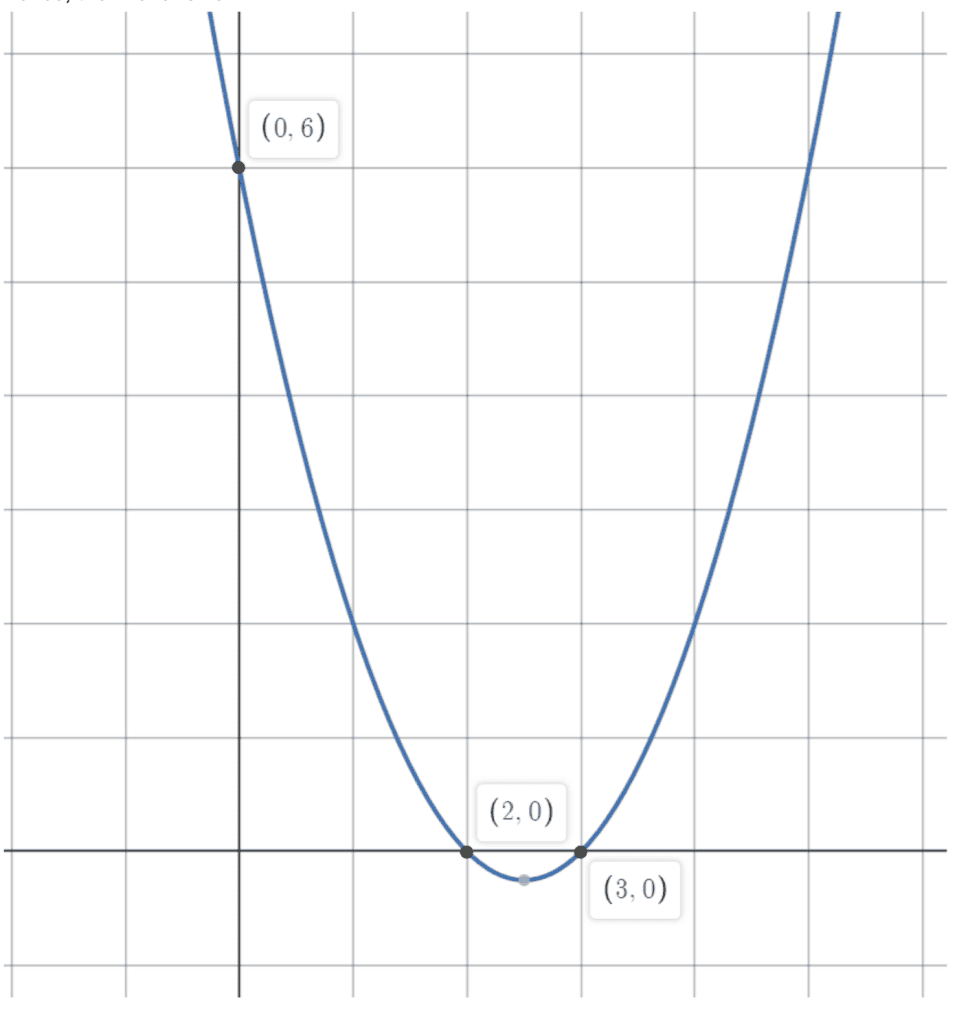
Sketch the graph of 𝑦 = 𝑥2 – 5𝑥 + 6, labelling all axial intercepts.
3 marks
Question 3
A student is given a box containing 6 different chocolates. The student randomly chooses 2 of these chocolates. How many different combinations of chocolates are possible?
2 marks
Multiple choice
Your multiple choice questions (MCQs) should always be CAS active. Though MCQs may sound easier, in Maths Methods this is absolutely not the case! Here are some reasons why:
- MCQs are only worth 1 mark each. However, the actual question sometimes involves 2 or 3 marks of working, so MCQs can be a massive time waster.
- Even if you know “a” correct answer, you may not see it as one of the options. You need to be familiar with different ways of representing the same answer!
Here are some general tips to help you out for MCQs. Try to integrate these tips into your practice SACs.
- The only thing that matters is your final answer. Learn CAS shortcuts that will give you the final answer straight away.
- Develop a sense of common traps students might fall into. It is likely the other options will include some of these mistakes.
Question 1
Consider a cubic graph that passes through the coordinates (-3, 0), (0, 0.6), (0.25, 0) and (4/3, 0). A possible antiderivative of this graph is:
A. \frac{x}{120}(18x^3 + 34x^2 - 159x + 72)
B. \frac{1}{20}(12x^3 + 17x^2 - 53x + 12)
C. \frac{1}{20}(36x^2 + 34x - 53)
D. \frac{1}{120}(12x^4 + 17x^3 - 53x^2 + 12x)
E. (x + 3)(4x - 1)(3x - 4)(3x - 5)
Question 2
A circle has the equation 𝑥2 + 𝑦2 – 4𝑥 + 6𝑦 – 3 = 0.Which of the following options describes the properties of this circle?
| Centre | Radius | |
|---|---|---|
| A | (2, -3) | 4 |
| B | (-2, 3) | 16 |
| C | (4, -6) | 9 |
| D | (-2, 3) | 4 |
| E | (2, 3) | 16 |
Question 3
If A and B are independent events, Pr(A) = 0.3 and Pr(B) = 0.5, what is the value of Pr(A ∪ B)?
A. 0.90
B. 0.8
C. 0.75
D. 0.65
E. 0.6
Not sure if you’re prepared for everything in VCE Maths Methods? Read our comprehensive post about everything you need to know!
Application questions
Application questions will involve using techniques you learn into real-world modelling scenarios. These questions often require a lot of reading, and this can pose its own issues.
Here are some of our tips to handling application questions.
- Diagrams are usually quite helpful. Sometimes, one will be provided. However, if it isn’t, consider drawing one for yourself.
- The key to success is knowing how to relate words into mathematical concepts. This is the key skill to work on during your practice SACs.
- These questions usually have multiple components (part a, part b etc.). If you can’t answer one component, make sure to still try the later ones!
Here’s one example of an application question that could come up in your Maths Methods Unit 1 and 2 Practice SACs.
Question 1
A research group is monitoring the population of foxes in a forest. The group models that the population of foxes is given by F= –4e-0.05t + 7, where F is the number of foxes in thousands, and t is the number of years after monitoring begins.
a. Find how much time it takes for the fox population to double after monitoring begins, correct to the nearest month.
2 marks
b. State what will happen to the fox population in the long term.
1 mark
This same research group observes that the fox population is related to the rabbit population. The rabbit population, in thousands, is given by R = 3e-0.2t + 5
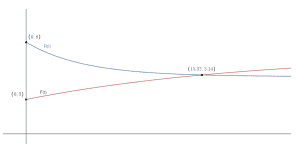
c. Sketch the graphs of R(t) and F(t) on the same set of axes over an appropriate domain. Label any axial intercepts and points of intersection, correct to 2 decimal places where necessary.
3 marks
d. Comment on the difference between the population change over time in the rabbit and fox population.
1 mark
3. Interpret what the point of intersection shows in the context of this modelling scenario.
1 mark
What’s next after smashing your VCE Maths Methods SACs exams? Read our tips to ace your end of year VCE Maths Methods exams!
Answers
Here, we will go through the answers to these questions. However, we will also point out some takeaway messages. You should think about what key learning lessons you can get out of the Maths Methods Unit 1 and 2 Practice SACs you complete.
If you need some help understanding the following solutions, we’ve got a fantastic team of Melbourne tutors who can support you!
Short answer
Question 1a
This is an example of the factor theorem. Without notes, you will need to use cues in the question to help you determine which concept to use.
- In this question, we have the word factor as well as a polynomial. Together, this suggests we should use the factor theorem.
Then, it’s a matter of correctly applying the concept. With smart use of brackets, we can minimise the risk of arithmetic errors.
If (𝑥 – 2) is a factor, then when we substitute in 𝑥 = 2, the polynomial should equal 0.
(2)3 + 2 \times (2)2 – 42 – 8 = 8 + 8 – 8 – 8
=0 as required (1 mark)
Takeaway messages:
- Use cues in the question to help you remember which concept to apply
- Use brackets and mathematical operators to help prevent arithmetic errors
Question 1b
The word hence means that you will want to use the answer to the previous question to answer this question. Otherwise, you will just want to be careful with correct arithmetic to arrive at the correct answer.
𝑥3 + 2𝑥2 – 4𝑥 – 8 = (𝑥 – 2)(a𝑥2 + b𝑥 +c) (1 mark)
𝑥 \times a𝑥2 = 𝑥3 so a = 1
–2 \times c = –8 so c = 4
𝑥3 + 2𝑥2 – 4𝑥 – 8= (𝑥 – 2)(𝑥2 + b + 4)
–2𝑥2 + b𝑥 \times 𝑥 = 2𝑥2 so b = 4
𝑥3 + 2𝑥2 – 4𝑥 – 8 = (x – 2)(𝑥2 + 4𝑥 + 4) (1 mark)
0=(𝑥 – 2)(𝑥 + 2)2
∴𝑥 ± 2 (1 mark)
Takeaway messages:
- The command word “hence” means you should use the answer from the previous question.
- You might also see “hence, or otherwise.” This means you can choose to use your own method if you would like.
Question 2
First of all, recognise that this is a quadratic. This is a polynomial with a leading term of 2.
You could convert this into turning point form, however we do not need to manipulate this equation at all. These are the sorts of time saves you should be looking for in your practice SACs!
For 𝑥-intercepts, let 𝑦=0
𝑥2– 5𝑥 + 6 = (𝑥 – 3)(𝑥 – 2)
Therefore, co-ordinates are (2,0) and (3, 0)
For 𝑦-intercepts, let 𝑥=0
Co-ordinate is (0, 6)
Leading term is 𝑥2, so shape is concave up.
Hence, the final answer is:
Note how we don’t label the turning point — this is because we do not need to.
1 mark — shape
1 mark — 1 label correct
1 mark — all labels correct
Takeaway messages:
- Practice saving time in your Maths Methods Unit 1 and 2 Practice SACs!
- Make sure you know what the question asks for and what the question is not asking for.
Want to know what VCE Maths subject will boost your ATAR? Read our breakdown of each VCE Maths level!
Question 3
Note the word combinations. This should be a cue to use the equation nCR = \frac{n!}{r!(n-r)!}
\frac{6!}{2! × 4!} = \frac{6×5×(4×3×2×1)}{(2×1)(4× 3×2×1)} (1 mark for reasonable working)
= \frac{6×5}{2}
= 15 (1 mark)
With some smart manipulation, we can simplify this.
Takeaway messages:
- Memorising equations will likely form a part of your CAS-free practice. You may or may not be given a formula sheet – make sure you know this before your Maths Methods Practice SACs
- With some smart arithmetic, it’s possible to reduce a complicated mathematical expression into something more workable
Check out our 25 practice exam questions for VCE Maths Methods!
Multiple choice
Question 1
Straight away, you can eliminate B and C. This is because the antiderivative of a cubic is a quartic. This is something you should train yourself to recognise for other types of MCQs!
Two options of completing this question include
- Finding the equation of the cubic, and then determining the antiderivative of that equation, or;
- Differentiating A, D and E and seeing the resultant graph.
Both of these options work, and will get A as the correct answer.
Takeaway messages:
- When you practice MCQs, see if there are multiple ways of approaching the same question, since one way might be faster than another!
- If you performed differentiation instead, you would reach C
- If you determined the equation of the cubic only, you would reach B
Question 2
Doing this by hand is certainly possible, perhaps just tedious. Instead, we can use the CAS to either:
- Convert the equation into (𝑥 – 2)2 + (𝑦 + 3)2 = 16, or;
- Sketch the circle
Either way will reveal that the answer is A.
Takeaway messages:
- “The previous answer was A, therefore this answer cannot be A.” This is nothing more than a schoolyard rumour!
- Remember that 16 = r2 (not just r!). See how some of the other answers refer to r = 16. These are the types of distractors you’ll see on multiple choice!
Question 3
Pr(A ∪ B) = Pr(A )+ Pr(B) + Pr(AB)
=0.3 + 0.5 + (0.3 \times 0.5)
=0.65, hence D
Takeaway messages:
- If A and B were mutually exclusive events, the correct answer would be B.
- If you forgot the equation for independent events, you would also end up with B.
- Trying to appreciate how the other options in multiple choice come up can help you avoid these mistakes
Find our 7-step night routine before your Maths Methods exam!
Application question
Part a
What do we actually need to find? Well, the question tells us to “Find how much time it takes” – this means find the value of t.
What else is the question asking? “…the fox population to double…” means that the value of F is doubled, and “after monitoring begins,” refers to t=0.
Therefore, we need to find the value of t when the value of F is doubled compared to the value of F when t = 0.
After this, we can compute the maths:
F(0) = 3, therefore need to solve F(t) = 6 for t
6 = –4e-0.05t + 7 (1 mark)
t = 27.73
Takes 27 years and 9 months for initial fox population to double (1 mark)
Takeaway messages:
- For application questions, your final answer usually has some real world relevance (i.e. leaving it as t = 27.73 is likely insufficient).
- Knowing how to “translate” words to mathematics is a key skill in application questions
Part b
“Long term” is interpreted as “very large t values.”
If we graph this on the CAS (or using algebra), there is an asymptote at 7.
In the long term, the fox population will approach, but not exceed, 7000 foxes (1 mark)
Part c
This is similar to the earlier graphing question, however this time we need to define an “appropriate domain.” Here, an appropriate domain would be t >= 0,as we don’t know anything before monitoring began.
1 mark for shape
1 mark for reasonable domain (i.e. t0 )
1 mark for all correct labels
Takeaway messages:
- Pay attention to domains, both domains that are explicitly stated or domains that are implied (like here)
- As long as you answer in relation to the context, you can use observations from graphs.
Part d
The fox population increases over time, but the rate of increase gradually slows. In contrast, the rabbit population decreases over time, though the rate of decrease gradually slows (1 mark)
Part e
Here, recall what the variables represent:
- T is the time after monitoring begins
- R and F are the rabbit and fox populations
In this case, t = 15.32 and R = F = 5.14
So the answer is:
After 15.32 years, the rabbit and fox populations are the same size at 5140 animals (1 mark)
Takeaway messages:
- Did you remember that F and R refer to the population in thousands? Pay attention to units!
Want more past papers to prepare for your Maths Methods Unit 1 and 2 Practice SACs? Check out our compiled list of VCE Maths Past Papers!
Are you looking for some extra help with working through VCE Maths Methods Unit 1 and 2 Practice SACs?
We have an incredible team of VCE tutors and mentors!
We offer specialised maths tutoring in Melbourne with expert tutors! Get in contact today to secure your expert coach.
We can help you ace your VCE Maths Methods Unit 1 and 2 Practice SACs and ace your upcoming VCE assessments with personalised lessons conducted one-on-one in your home or online!
Looking for a local tutor in Footscray? Or needing support for the VCE in Doncaster? We offer one-on-one tutoring, in your home or online!
We’ve supported over 8,000 students over the last 11 years, and on average our students score mark improvements of over 20%!
To find out more and get started with an inspirational VCE tutor and mentor, get in touch today or give us a ring on 1300 267 888!
Kevin Chen recently completed his Bachelor of Biomedicine at the University of Melbourne. He is now undertaking an Honours year, where he is investigating the rise of hospital superbugs. Kevin lives by the motto “smiles go for miles!”