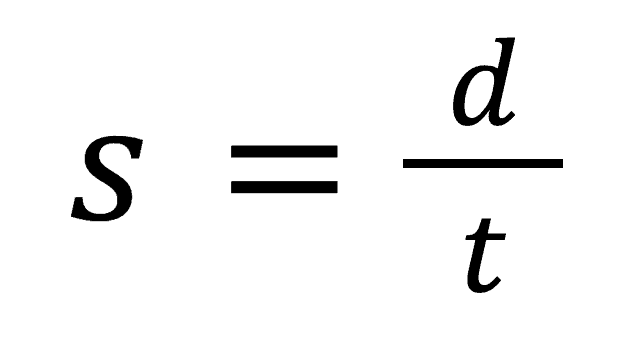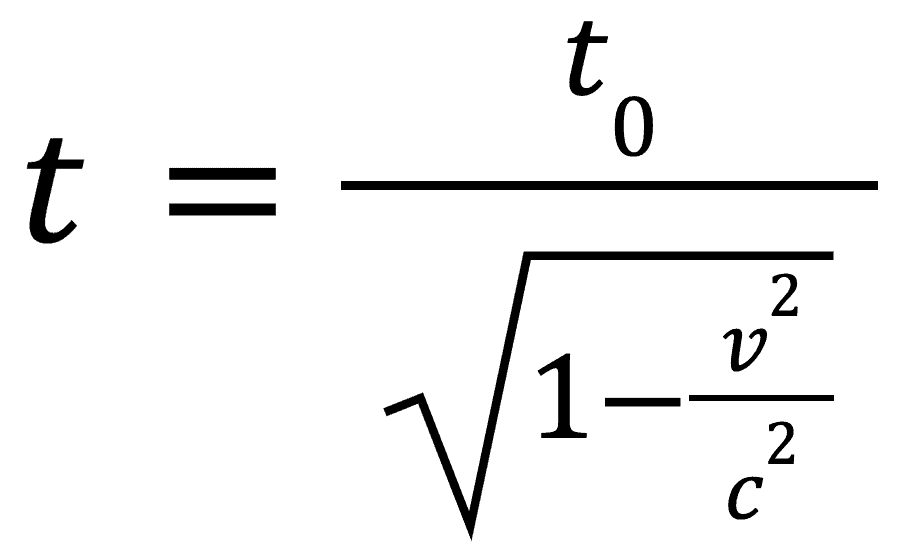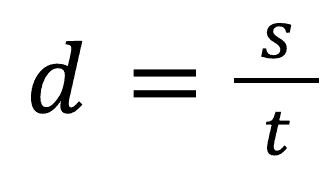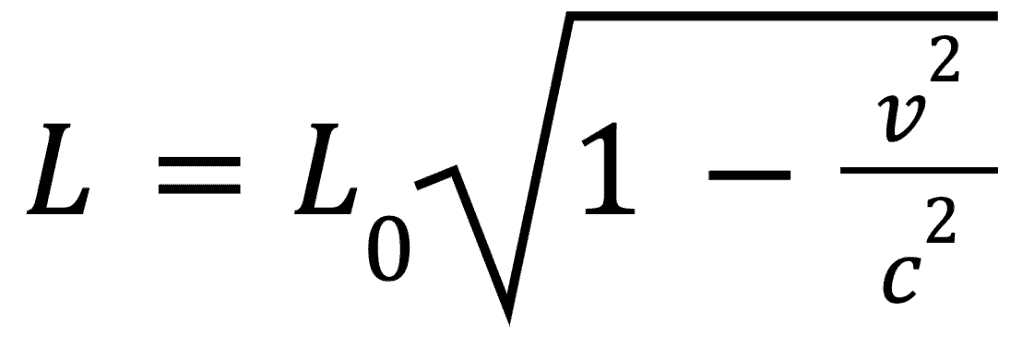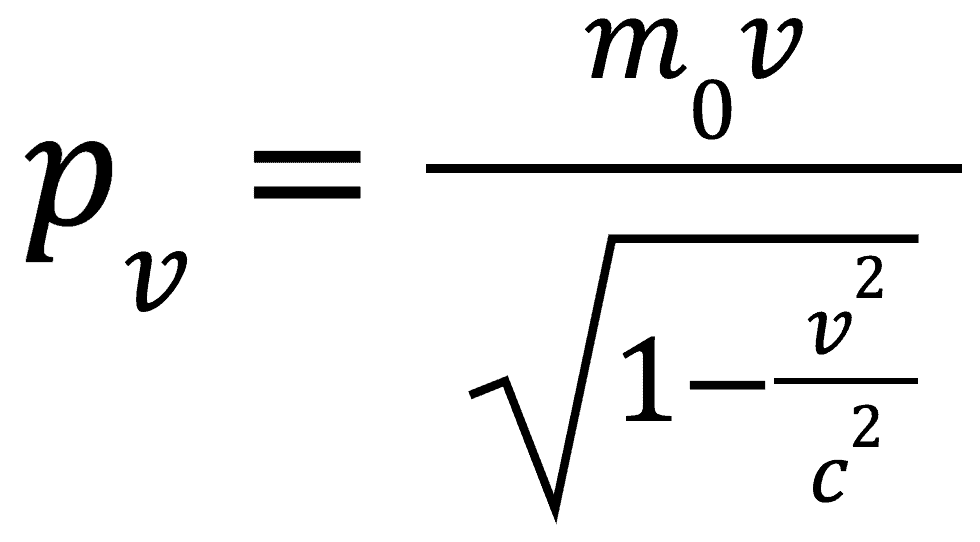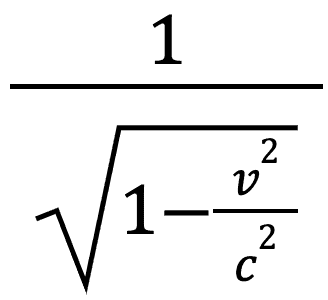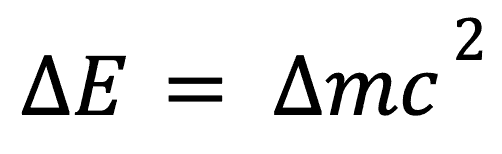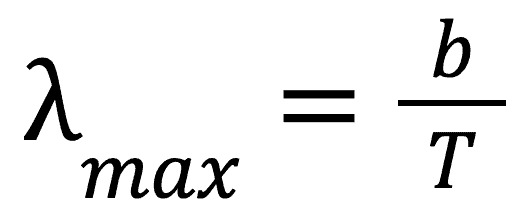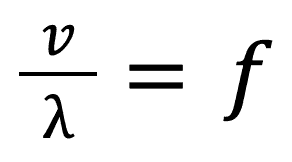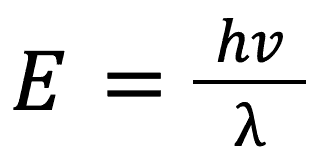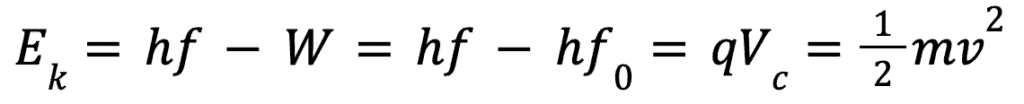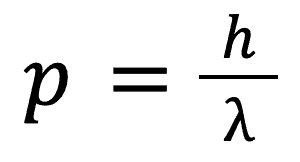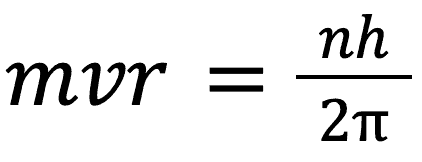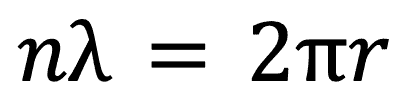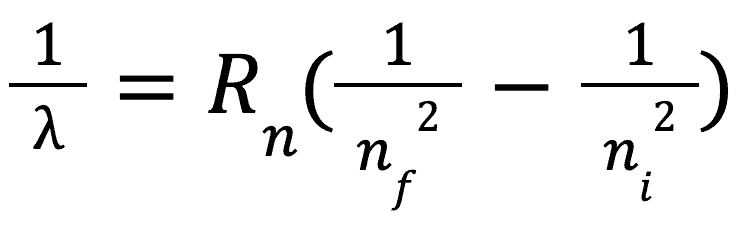So you’ve made it through the classical section of Grade 12 Physics, meaning now we can move on to modern physics in QCAA Physics Unit 4.
This section of the course, while being less math and equation heavy, can be harder to get your head around as some of the concepts don’t make much intuitive sense. Don’t panic though! We’re here to work through the concepts together and make them easier to understand.
We should also note before we get started that this QCAA Physics Unit 4 guide is only an overview of the topics and can therefore not go into all the details of the topics — so make sure to do further reading on anything you need clarification for!
Now what are you waiting for? Let’s get started on QCAA Physics Unit 4!
Topic 1: Special Relativity
Topic 2: Quantum Theory
Topic 3: The Standard Model
Topic 1: Special Relativity
Special Relativity: A qualitative understanding
You should remember from your earlier Physics studies that speed is equal to distance divided by time or in equation form:
Now imagine that you are driving at 90km per hour down a road. Next to you is another car traveling at 100km per hour in the same direction.
From your perspective the car next to you is moving forwards at only 10km per hour. This idea is known as relative motion and is useful for calculating speeds of things relative to other things.
We also know from our studies of electromagnetism that light is an object that moves (though it has no mass). We know from this that light moves at a speed of:
Now what if that speed of light is constant, no matter how fast you are moving?
This, along with the idea that the laws of physics are the same in all reference frames is what up-and-coming physicist Albert Einstein postulated in 1904 which led to his theory of special and eventually general relativity.
It should be noted that this only holds true when talking about a frame of reference that is not accelerating, what is known as an inertial reference frame. We will only deal with these types of reference frames in the course.
Take our previous example of the two cars once again. Let’s add to the situation a large light bulb very far ahead of the cars.
Let’s say that the lightbulb begins emitting light at the point where both of the two cars are directly next to each other. If the speed of the light is the same for both drivers then that means that the light from the light bulb will reach the driver of the faster car before the driver of the slower car, even though the light was emitted at 1 point in time.
This would imply that the drivers of the cars are perceiving time differently. And because speed is distance over time, they must also be perceiving distance differently.
At this point you may find this concept quite confusing as it is not something that we ever experience on a daily basis and therefore is quite unintuitive.
If you wish for more information on this for QCAA Physics Unit 4, we highly recommend checking out the crash course on special relativity found here!
Time Dilation
In our previous example with the two cars we found that the faster you are moving the less time you measure.
This can be represented as an equation which measures this difference known as the time dilation. It is as follows:
Where v represents the velocity you are traveling, c represents the speed of light, t represents the dilated time and t0 represents the proper time.
The proper time will be the time measured by the moving observer and will therefore be smaller than the dilated time. The dilated time gives how long an event would take in the inertial reference frame of a stationary observer.
You can see from this equation that time dilation only really applies when we are moving at extremely fast speeds that are comparable to the speed of light — this is why we don’t really experience this phenomena in our daily lives.
Length Contraction
We determined from the first section that if two observers experience time differently, they must also experience distance differently. Let us reexamine that claim through the following equation:
We know that in the case of two observers, 1 moving and 1 stationary, the moving observer will experience a shorter time interval.
If the two observers are to agree on their speeds, then the moving observer must therefore experience a shorter distance — this is known as length contraction. It is important to note that length contraction only applies in the direction of the objects movement as shown in the below figure:
Image sourced from Wikimedia Commons archive
Similar to time dilation, there is a formula explaining this phenomena:
Where L is the contracted length and L0 is the proper length. Contrary to the time dilation equation, the stationary observer in this instance will measure the proper length.
It should be noted that from the perspective of a stationary observer, the moving observer appears contracted while from the perspective of the moving observer, everything else appears contracted.
Simultaneity
Simultaneity is when two observers measure two events as happening at different points in time, i.e. the events being simultaneous or not.
This isn’t necessarily a concept of special relativity but more a consequence of time dilation and length contraction.
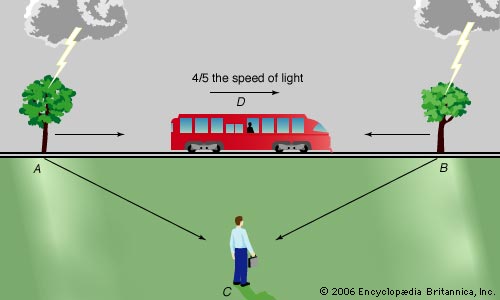
Imagine a situation where you stand next to some train tracks, equally far away from two trees. Let’s say that a train travelling at 4/5 the speed of light left to right passes you at the exact moment that both trees are struck with lightning (from your perspective).
From the train’s perspective the tree on the right is hit first, then the tree on the left. How is this possible? You can see this situation in the below diagram.
Image sourced from Encyclopædia Britannica
The answer to this paradox is that both of them are right, in their own perspectives. They just perceive the events to happen at different times because of their difference in speeds.
Paradoxes and Solutions
There are a couple of important paradoxes that you should be able to explain that will most likely come up on your exams. The first is known as the Twins paradox.
The Twins paradox
Imagine that there are two twins on earth, they are both the same age. One of the twins leaves earth on a spaceship for some amount of time and then returns. When he returns he is noticeable much younger than the twin that stayed on Earth, how is this possible?
This paradox can be explained as a consequence of time dilation in special relativity. The Older twin experienced dilated time and therefore more time than his younger twin.
The Barn Door paradox
The second paradox is a bit more complicated and is known as the barn door paradox.
Imagine that there are two farmers, one inside of a 10m long barn and 1 with a 15m long ladder outside of the barn. Both of the barn doors are open, however, the farmer inside of the barn can pull a lever to close the doors once the ladder is inside.
The idea of the paradox is that the observer with the ladder begins moving at a relativistic speed, such so that the ladder in the stationary observers perspective is now shorter than the barn. However, from the moving perspective it is the barn that contracts in length and therefore the ladder does not fit in the barn.
So which perspective is correct?
Similar to the last paradox the answer is that both of the perspectives are correct and the paradox only arises by the misunderstanding of absolute simultaneity.
Relativistic Momentum
Something that we have left unmentioned up until this point is momentum. For the conservation of momentum to still be valid we need to modify our understanding of the momentum equation.
Instead of representing it as:
We instead show it as:
With this modified version of our momentum equation the conservation of momentum now makes sense.
You will note that all of our special relativity equations contain the term:
This is known as the Lorentz factor and is sometimes referred to as γ (gamma).
Mass energy equivalence
Perhaps the most famous equation in physics, the mass energy equivalence equation shows how mass has intrinsic energy to it which can be described as follows:
Topic 2: Quantum Theory
Before we start this section of the QCE Physics Unit 4 course, it should be mentioned that this section contains reference to quite a few different famous experiments — we won’t quite have time to go into great detail about all of these so feel free to do some further research on these.
Black Body Radiation
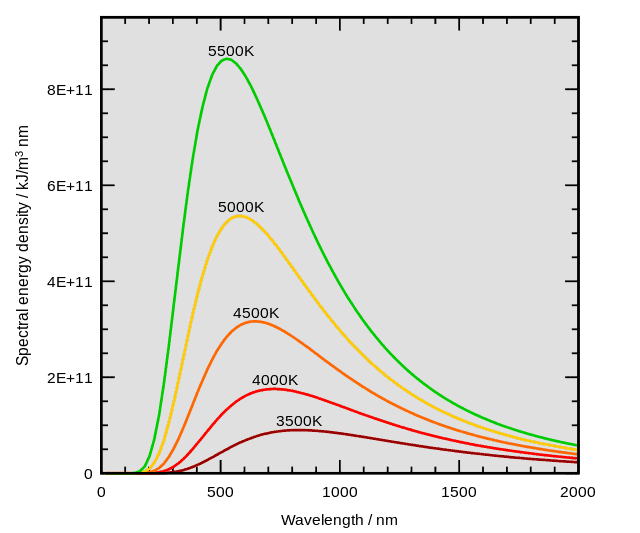
A black body is a theoretical object that can perfectly absorb and emit radiation of any wavelength. When this object’s temperature is increased, it emits a spectrum of wavelengths which follows the below shape:
Image sourced from Wikipedia
You can see from this image that each temperature gives its own characteristic curve. The most commonly occurring wavelength for each of these temperatures can be calculated as follows.
Where lambda is the wavelength, T is the temperature of the body and b is Wien’s displacement constant (found on formula sheet).
Ultraviolet Catastrophe
You will notice that on the graph describing Wien’s law, it is predicted that at high temperatures there will be very low wavelengths produced such as UV and even gamma rays. This caused a great issue in physics at the time as it was found that more low wavelength particles were supposed to be produced than the energy used to make them thereby violating the conservation of energy.
It was this issue known as the ultraviolet catastrophe that lead to the discovery of quantised energy levels
Planck’s Quanta
As a solution to the ultraviolet catastrophe, german physicist Max Planck proposed that rather than giving off a continuous spectrum of radiation, atoms could only emit energy in discrete packets known as quanta. These quanta would later become known as photons.
Planck discovered that these energy quanta could be measured using the following formula:
Where E is the energy in joules, f is the frequency of light emitted and h is Planck’s constant (found on formula sheet).
You can also expand on this formula by combining it with another that you should have learnt in Grade 11, that is:
Combining these two formulas you get:
This discovery led to the resolution of the ultraviolet catastrophe as it explained that energy changes are due to electrons moving between discrete energy levels rather than continuous distances.
The Photoelectric Effect
Heinrich Hertz conducted an experiment in 1887 demonstrating a phenomena which has now become known as the photoelectric effect. Without going into to much detail as to the experimental setup, Hertz essentially discovered that he could eject electrons from a metal plate by shining light above a specific frequency on it.
This specific frequency he called the threshold frequency denoted by f0.
Using Planck’s aforementioned formula, the energy binding the electron to the plate can therefore be described as E = hf0. This is known as the work function and is represented as W.
The kinetic energy of the electrons can be calculated as follows:
Where Ek is the charge, m is the mass, v is the velocity and Vc is a special quantity known as the cut-off voltage which is a certain voltage that makes the current equal to zero.
The Compton Effect
Again without specifying the experimental setup, Arthur Holly Compton discovered that photons had momentum. He also discovered that this momentum could be calculated as follows:
But this looks a little strange, how can a photon have a wavelength? This is perhaps one of the strangest discoveries in physics and leads to the conclusion that light can be described as both a particle and a wave.
Atom Models
There are 3 main models of the atom that you will need to understand for your exams (in QCE Physics Unit 4) and 1 other that is interesting to know which we won’t touch upon here (Heisenberg probability model if you are interested). We will begin with the first, Rutherford’s model.
Rutherford’s Model
Rutherford’s model of the atom describes a large mass nucleus being orbited by low mass electrons. In this model it is believed that the coulomb force is analogous to gravitation in the planetary system.
Within this model it is believed that when an atom is hit by a photon it becomes excited causing an electron to jump up an energy level. This form of the atom is unstable causing the electron to jump back down an energy level thereby releasing a photon of a specific wavelength in the process.
Even though this seems like a tonne-load of information, when you know how to take effective science study notes, it becomes a piece of cake to revise for Physics!
Bohr’s Model
We will now look at Bohr’s model of the atom.
Similar to Rutherford’s model, the atom is described as a large mass nucleus being orbited by low mass electrons. It is also described as having electrons in certain fixed orbits.
The biggest issue of Rutherford’s model that was addressed by Bohr is the stability of the atom. In Rutherford’s model, the electrons are undergoing circular motion and would eventually lose their energy and spiral into the nucleus.
Neils Bohr instead postulated that the electrons are in fixed energy levels and do not radiate energy.
Something else that is important to note here is that the angular momentum of the electrons in the Bohr model is quantised, that is:
L = mvr
where L is the angular momentum and
de Broglie Wave Model
The final model that we will look at is the de Broglie wave model. It describes particles, similar to light, as having a wave particle duality.
With this in mind it describes the electrons around a nucleus as being waves and that in each energy level there can fit an integer number of wavelengths around the energy level. In equation form this is:
Rydberg Series
The Rydberg series is simply a way of describing the energy level differences in atoms. It should be noted that this only works for hydrogen, helium, lithium and beryllium atoms. The formula is as follows:
where Rn is rydberg’s constant (found on formula sheet), ni is the energy level you are starting at (n can only be an integer i.e n=1,2,3,4…) and Nf is the energy level you are finishing at.
Topic 3: The Standard Model
The standard model is a way of describing and classifying the four fundamental forces of our universe and the smallest possible elementary particles that make it up.
The four forces are as follows (ranked from strongest to weakest):
- Strong nuclear force (hold nuclei together)
- Weak nuclear force (responsible for radioactive decay)
- Electromagnetic Force
- Gravity
These forces act between bodies of matter and are mediated by one or more particles which are known as bosons. These force carrying bosons are also called Gauge bosons.
Each of the fundamental forces has its own gauge boson, except for gravity. The following table describes the gauge bosons and how they relate to the forces.
| Force | Particles | Distance/Strength | Gauge Bosons |
|---|---|---|---|
| Strong Nuclear Force | Quarks only | Increases up to a point | Gluon (g) |
| Weak Nuclear Force | Quarks and Leptons | Smaller distance than the strong force | W (W+,W-) and Z (Z°) bosons |
| Electromagnetic Force | Charged Particles | Infinite range | Photon (γ) |
| Gravitational Force | Anything with mass | Infinite range | Graviton, not yet discovered/confirmed |
The elementary particles within the standard model can be seen below (note: you do not need to know about the Higgs boson in QCE Physics Unit 4).
Particle Interaction
A particle is a baryon/antibaryon if it is made up of 3 quarks or 3 antiquarks. If a particle is a baryon it has a baryon number of +1, if it is an antibaryon it has a baryon number of -1.
In all interactions the baryon number is conserved. Leptons have a baryon number of 0
A lepton has a lepton number of +1 while an antilepton has a number of -1. Lepton number is conserved in all interactions. Non-leptons have a lepton number of 0.
The main way that we will represent particle interactions is through what is known as a Feynman diagram. There are a few Feynman diagrams that you will need to know for your exam.
The axis of Feynman diagrams are space and time and they are read from left to right. The solid lines in the diagram represent particles, the wavy lines represent bosons. The vertices on the graph represent a particle interaction.
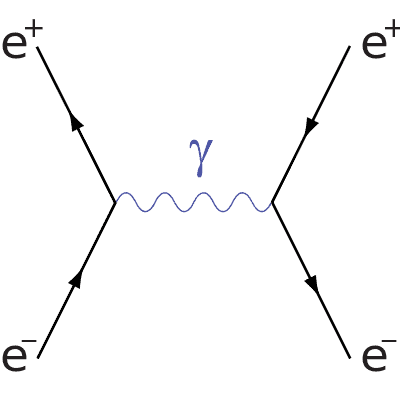
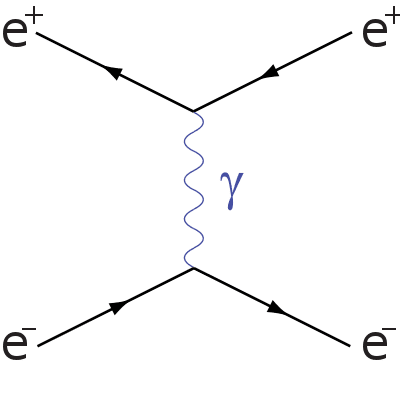
Electron-positron annihilation/production
The first Feynman diagram you will need is electron-positron annihilation/production, it is as follows:
Image sourced from Wikipedia
You can see from this diagram that the y-axis is space and the x-axis is time, you will notice that the antiparticles travel backwards in time, this is the same for all Feynman diagrams. You can see that an electron and positron collide, forming a photon before again producing an electron and positron.
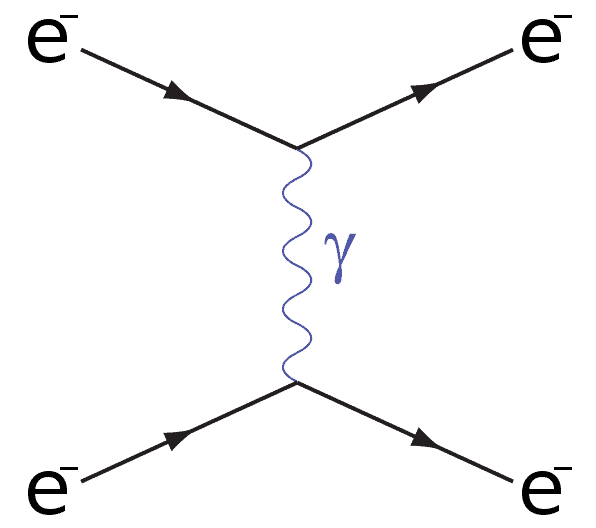
Repulsion
The next Feynman diagram that you will need is an electron-electron interaction also known as repulsion.
Image sourced from Wikipedia
You can see that as the two electrons get close, a virtual photon is emitted which mediates the electromagnetic force between the electrons causing them to repel one another.
Bhabha Scattering
This same Feynman diagram can be replicated replacing one of the electrons with a positron, this is known as Bhabha scattering.
Image sourced from Wikipedia
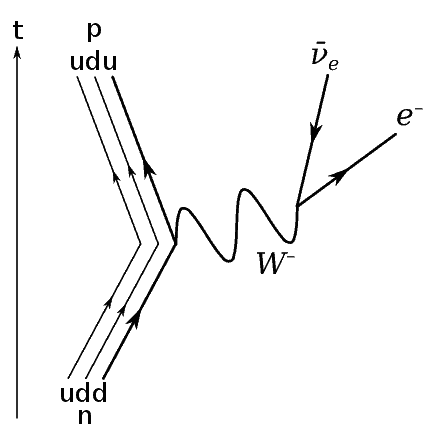
Neutron Decay
The final Feynman diagram that you will need is neutron decay. This Feynman diagram can be drawn in 2 ways, either by showing the particles, or by showing the quarks.
We will show the variant which shows the quarks. It can be seen below:
Image sourced from Wikipedia
Firstly, you will notice that the axes are the other way around in this example — this doesn’t change anything about the diagram, it is just to show that you draw these in any way.
Looking for Unit 3 Physics? Check out our guide for the year!
You’re a Physics student… of course you’re also a Chemistry student, struggling with Unit 4 Organic Chemistry? Or check out our Unit 4 Guide to Maths Methods!
As you can see one of the down quarks in a neutron decays into an up quark via the W–boson, turning the neutron into a proton while also producing an electron antineutrino and an electron.
Know exactly what marks you need to aim for in Unit 4 with our brand new QCE Cohort Comparison Tool!
Are you looking for some extra help with revising QCAA Physics Unit 4?
We have an incredible team of QLD Physics tutors and mentors!
We can help you master the QCAA Physics syllabus and ace your upcoming Physics assessments with personalised lessons conducted one-on-one in your home or online!
We’ve supported over 8,000 students over the last 11 years, and on average our students score mark improvements of over 20%!
To find out more and get started with an inspirational QLD tutor and mentor, get in touch today or give us a ring on 1300 267 888!
William Bye is a Content Writer at Art of Smart and is currently studying a Bachelor of Advanced Science with Honours (majoring in Physics) at the University of Queensland. He was part of the very first cohort in Queensland to go through the ATAR system and wishes to help other students to make this journey as easy as possible. Will enjoys his time playing guitar in a band with his friends and hopes to continue balancing his science and music for many years to come.