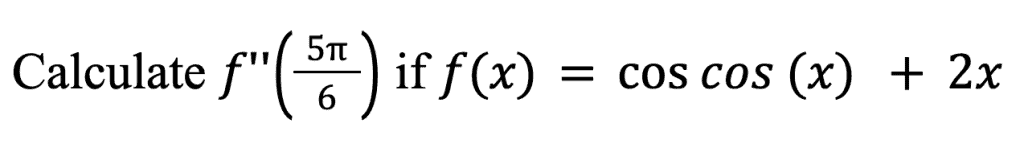Preparing to complete your QCAA Unit 4 Maths Methods IA3 Short Answer test? Look no further because we’ve got a range of questions you can use to study!
Alongside these 25 practice questions, we’ve got the answers which you can download once you’ve worked through the questions.
What are you waiting for? Let’s get started!
Short Answer Practice Questions
Question 1 (3 marks)
Consider the function f(x) = 8x2 – 2x3.
a) Determine where, in terms of x, the function is:
- Concave up
- Concave down
b) State the coordinates of the point of inflection (give your answer to two decimal places)
Question 2 (2 marks)
Determine all solutions to the equation sin sin (θ) = 0.5 in the domain 0 ≤ θ ≤ 3π.
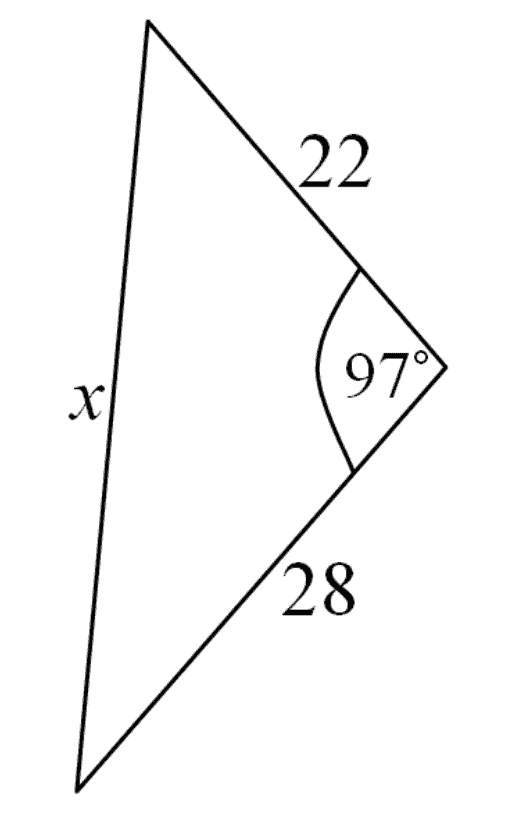
Question 3 (2 marks)
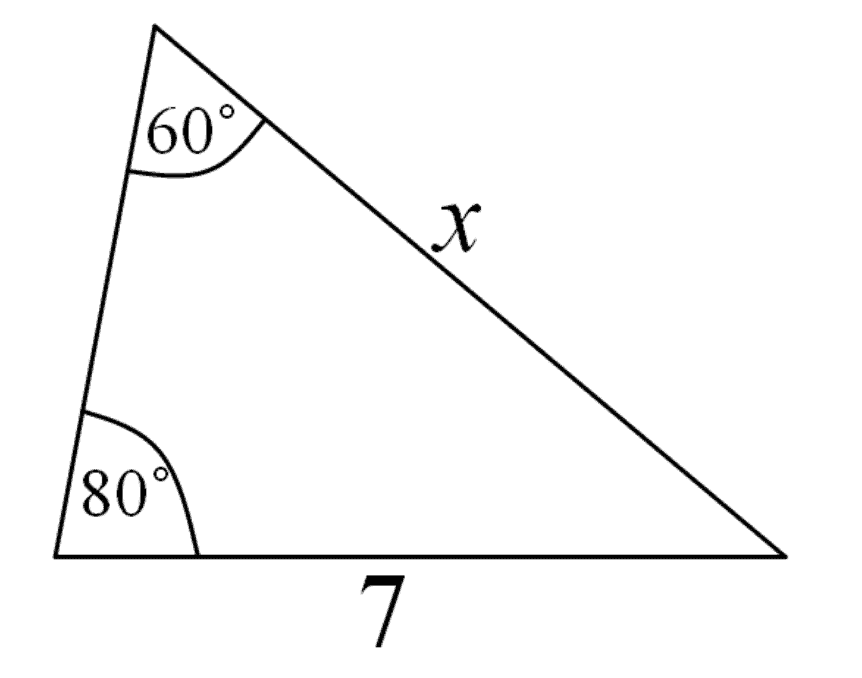
Find the length of the side labelled x. Give your answer to two decimal places.
Image sourced from Centre for Innovation in Mathematics Teaching
Question 4 (3 marks)
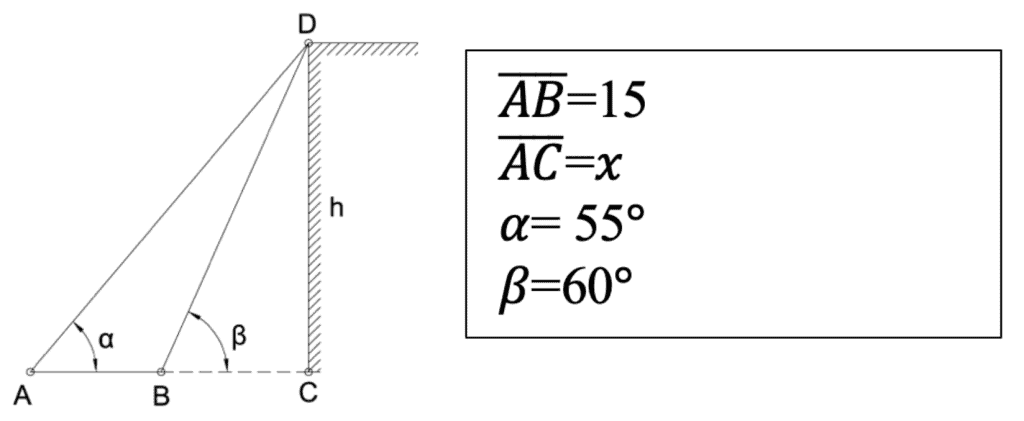
The angle of elevation to the top of a particular building is 55° from Point A, which is xm from the building. From Point B, which is 15m closer to the building, the angle of elevation to the top is 60°. What is the height of the building?
Image sourced from TheCivilEngineer.org
Question 5 (2 marks)
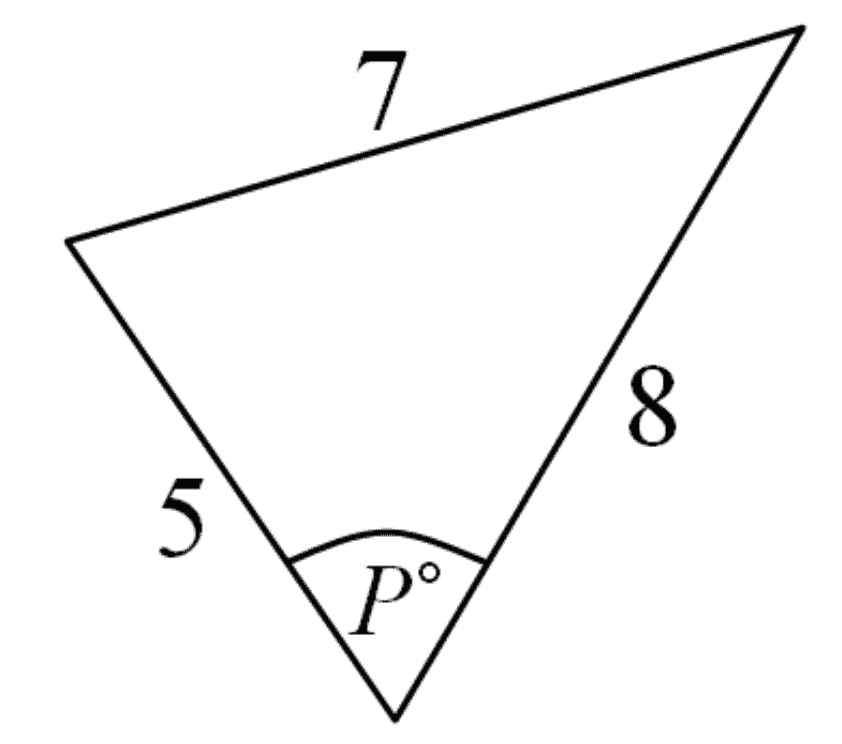
Find the size of the unknown angle
Image sourced from Centre for Innovation in Mathematics Teaching
Question 6 (4 marks)
An object travels in a straight line. Its displacement from the origin is xm/s, at time t seconds is given by the following function:
x(t) = 0.5ex + 2x – 0.5, 0 ≤ t ≤ 5
a. Determine an expression for the velocity of the particle as a function of time
b. Determine an expression for the acceleration of the particle as a function of time
c. Calculate the initial speed of the particle
d. Determine when and at what position the particle is at rest
Question 7 (2 marks)
Solve 2 sin sin (2x) – 2 = 0, 0 ≤ x ≤2 π
Question 8 (2 marks)
Solve the following:
2 cos cos (x) – √3 = 0, 0 ≤ x ≤ 3π
Question 9 (3 marks)
A new medication has been developed for the treatment of hay fever. In lab trials, the medication was found to be effective in 81% of the cases. Kim has been prescribed the medication. Letting X be the effectiveness of the medication:
a. Construct a probability distribution table for X
b. Determine E(X)
c. Determine the variance and standard deviation of X, correct to four decimal places
Question 10 (5 marks)
Sketch the graph of f(x) = xex + 2. Calculate and label the x and/or y-intercepts, stationary points and points of inflection. Giver your answers to two decimal places.
Question 11 (2 marks)
The probability of Jim hitting the centre of the dartboard is 0.65. What is the smallest number of darts he needs to shoot to ensure that the probability of him hitting the centre at least once is more than 0.8?
Question 12 (2 marks)
Amy has a math test that consists of 40 multiple choice questions which have 4 answer options each. She chooses her answers all at random. Let X be the discrete random variable that describes the number of answers she gets correct.
a. Determine the expected number of questions Amy has gotten correct.
b. Determine the standard deviation of the number of questions answered correctly. Give your answer to two decimal places.
Question 13 (3 marks)
Z, a binomial random variable, has a mean of 6.3 and a variance of 2.3.
a. Determine the probability of success (p). Give your answer to two decimal places.
b. Determine the number of trials (n). Give your answer to two decimal places.
Question 14 (4 marks)
A recent study has shown that 14% of the population has asthma. A sample of 20 people were tested for asthma. Let X be the random variable that represents the number of people who have asthma.
a. Determine P(X≤5). Give your answer to four decimal places.
b. Determine E(X) and SD(X). Give your answer to four decimal places.
Question 15 (6 marks)
Sketch the graphs of the following functions and state whether each function is a probability density function.
a. f(x) = ∫ 2(x + 2) – 6, 1 ≤ x ≤ 4, 0 elsewhere
b. f(x) = ∫ 0.5x – 2, 4 ≤ x ≤6, 0 elsewhere
Question 16 (2 marks)
Z is a normally distributed random variable, determine:
a. x given that P(Z > x) = 0.45, Z ~ N (14.5, 1.32)
b. n given that P(Z < n) = 0.67, Z ~ N (19, 2.12)
Question 17 (4 marks)
The amount of strawberries packed into one carton for a particular brand is normally distributed with a mean of μg and a standard deviation of 5g. The advertised weight of each strawberry carton is 300g.
a. Calculate the number of packets that will be under the advertised weight when μ = 310g. Give your answer to four decimal places.
b. Calculate the value of μ required to ensure that only 2% of packets are below the advertised weight. Give your answer to four decimal places.
Question 18 (4 marks)
James surveys 200 people and finds that 30 of them like mint ice-cream. Estimate the proportion of the population that likes mint ice-cream. Determine a 95% confidence interval. Give your answers to four decimal places.
Question 19 (2 marks)
On average, 30% of people spend at least 2 hours a day on social media. Using the normal approximation, determine the approximate probability that, in a sample size of 500, more than 45% of people have spent at least 2 hours a day on social media. Give your answer to three decimal places.
Question 20 (2 marks)
Find the mean of the following probability density function:
f(x) = ∫ 3x2 – 6x, 2 ≤ x ≤ 4, 0 elsewhere
Question 21 (3 marks)
Find the median of the following function
f(x) = ∫ 2x – 3, 4 ≤ x ≤ 6, 0 elsewhere
Question 22 (2 marks)
Question 23 (2 marks)
The probability of the train being late is 0.25. What is the probability that the train is on time at least once in the next four days?
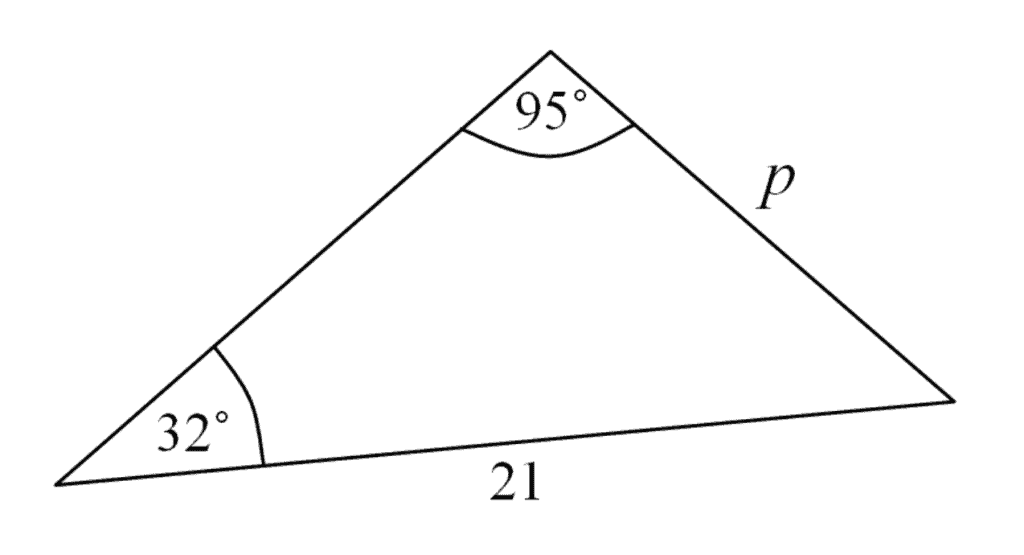
Question 24 (2 marks)
Find the length of the side labelled p. Give your answer to two decimal places.
Image sourced from Centre for Innovation in Mathematics Teaching
Question 25 (2 marks)
Find the length of the unknown side.
Image sourced from Centre for Innovation in Mathematics Teaching
BONUS QUESTION (2 marks)
If N = 450, n = 50 and p = 0.4, calculate:
a. the mean of the distribution.
b. the standard deviation of the distribution. Give your answer to two decimal places.
QCAA Unit 4 Maths Methods Short Answer Practice Solutions
Click here to download the solutions to the 25 practice questions above!
Curious to know how your marks compare with your cohort’s? Input your IA marks for Maths Methods in our QCE Cohort Comparison Tool to find out!
On the hunt for other QCAA Maths Methods resources?
We’ve created a bunch of helpful articles and practice questions for studying QCAA Maths Methods. Check them out!
- The Ultimate Term 3 Content Guide
- The In-Depth Summary for Maths Methods Unit 4
- Unit 3 IA2 Short Answer Practice Questions
- Download QCAA Maths Methods Practice Exam for External Assessment Revision
- How to Structure Your PSMT Report for QCAA Mathematical Methods
- QCAA Practice Questions for Unit 3 & 4 Maths Methods External Assessment
- How to Ace Your External Assessment for Mathematical Methods
Are you looking for some extra help with the QCAA Unit 4 Maths Methods Short Answer test?
We have an incredible team of QLD tutors and mentors!
We can help you master the Maths Methods syllabus and ace your upcoming Maths Methods assessments with personalised lessons conducted one-on-one in your home or online!
We support Maths tutoring throughout Brisbane and the Gold Coast!
We’ve supported over 8,000 students over the last 11 years, and on average our students score mark improvements of over 20%!
To find out more and get started with an inspirational QLD tutor and mentor, get in touch today or give us a ring on 1300 267 888!
Yalindi Binduhewa is an Art of Smart tutor based in Queensland and was part of the very first cohort to go through the ATAR system, so she knows exactly how fun and enjoyable it can be. She is currently studying a Bachelor of Medical Imaging (Honours) at QUT and is loving it. When she’s not doing uni-related stuff or tutoring, she’s hanging out with her friends, rewatching a show for the 100th time, or trying out new crafty projects and discovering that she doesn’t have a talent for everything.