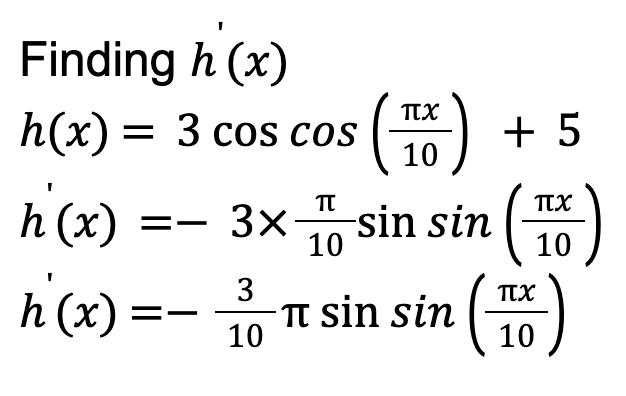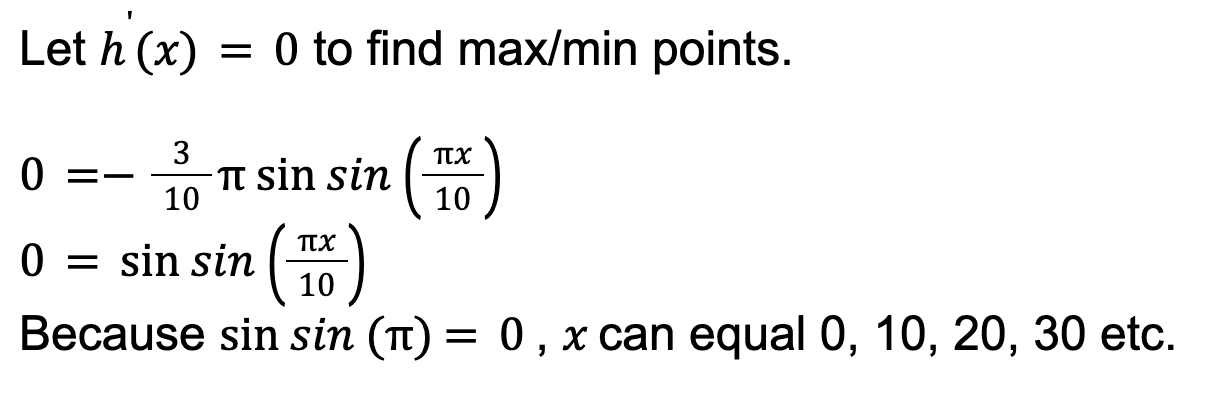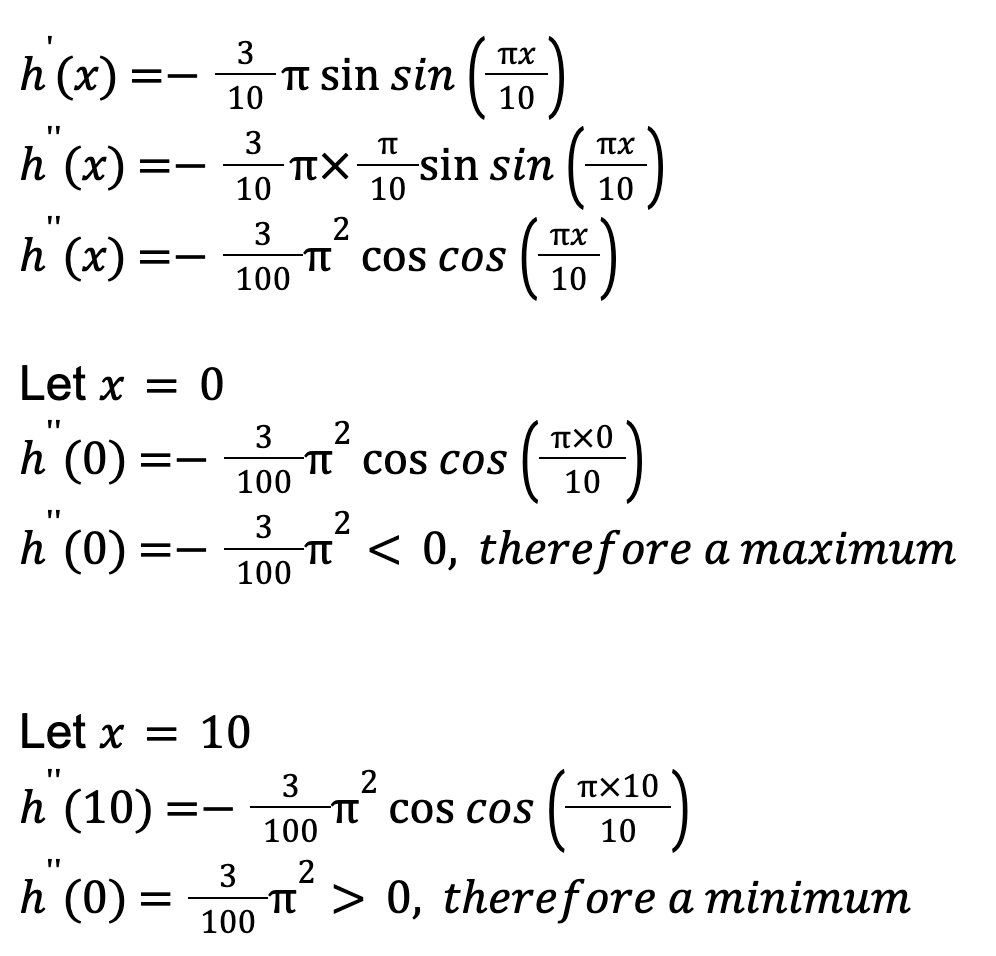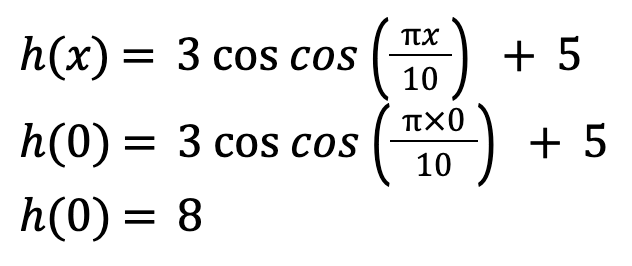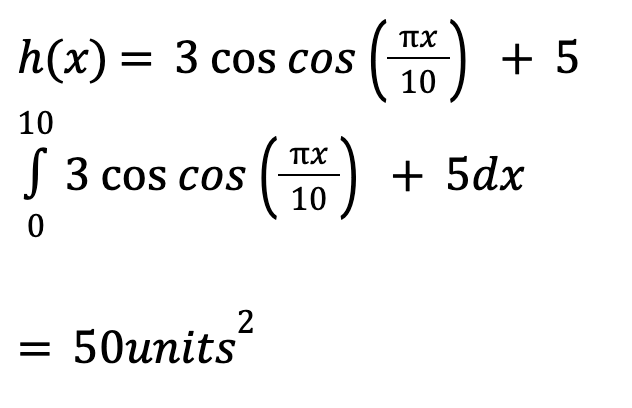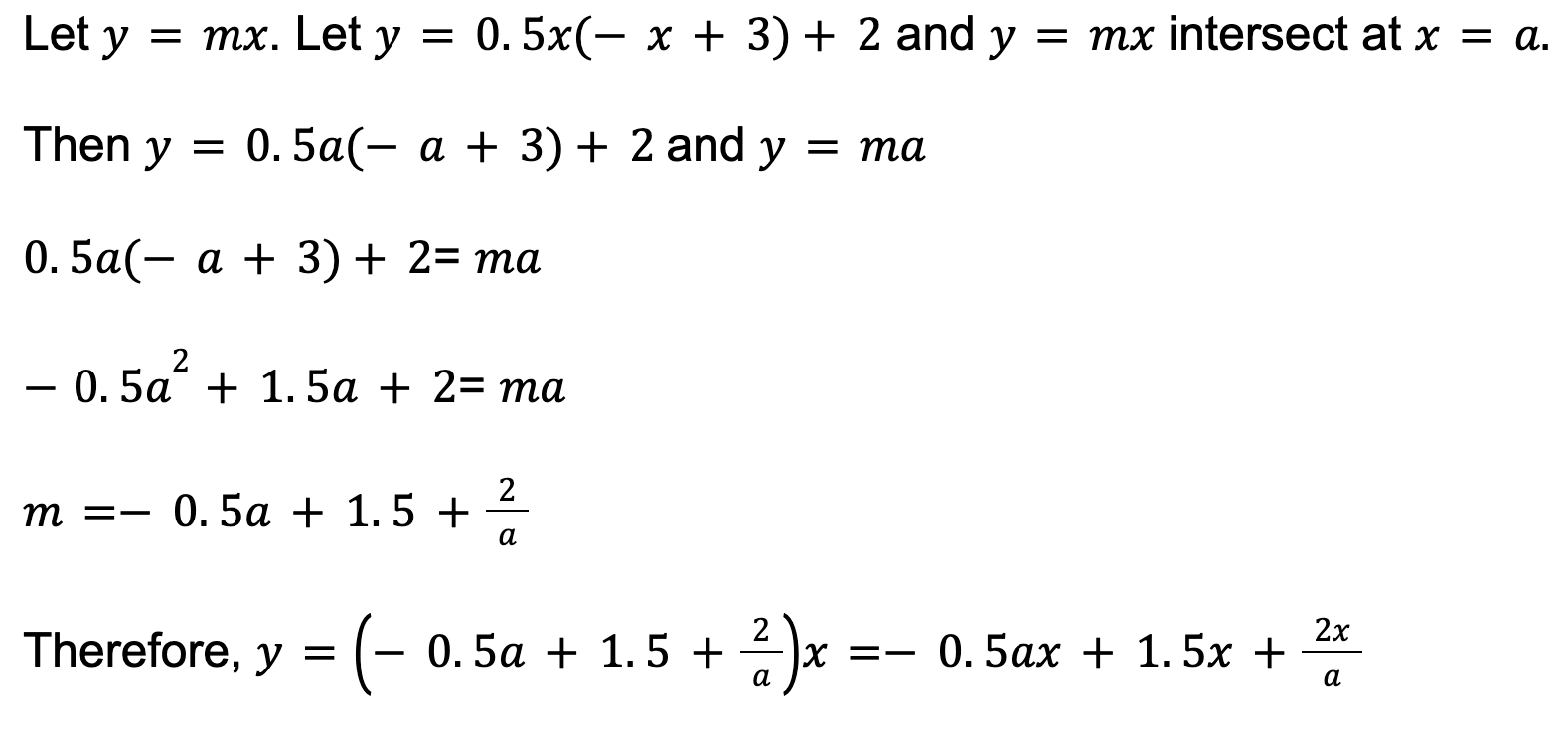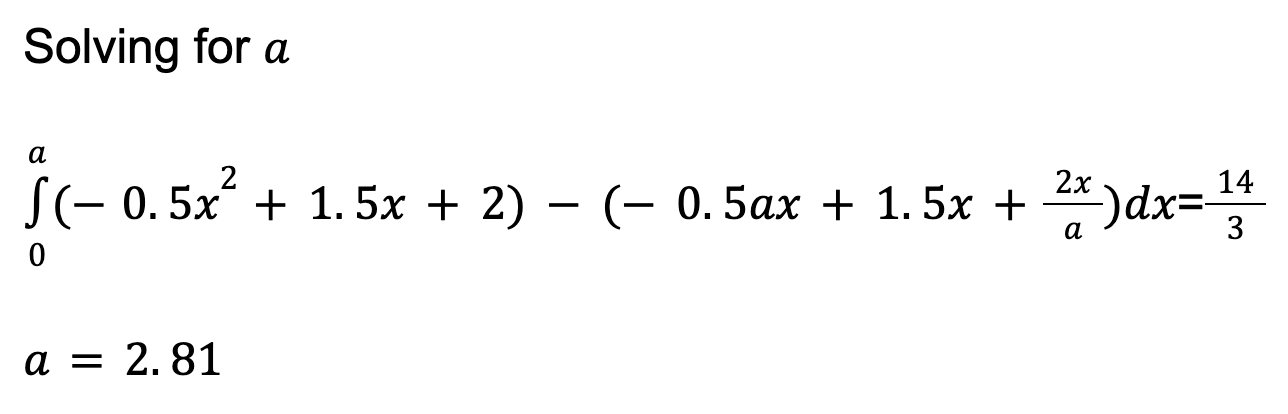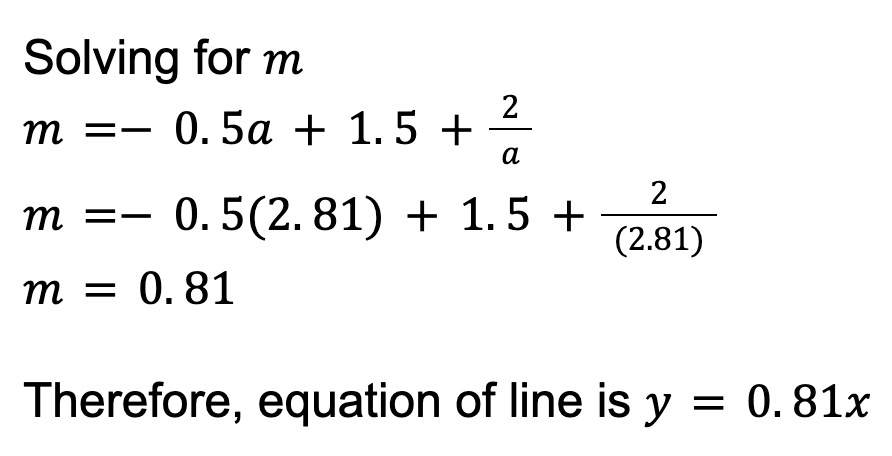Find yourself struggling with the last few questions of a Maths exam? These questions tend to be classified as “complex unfamiliar” ones, and are definitely a challenge to do.
There’s a lot more to these questions than meets the eye, so we’ll take you through a simple approach you can follow in order to tackle them!
What are you waiting for? Let’s get started!
What are Complex Unfamiliar Questions?
How do you answer Complex Unfamiliar Questions?
How do you prepare for Complex Unfamiliar Questions in your exam?
Worked Example 1 (Technology – Free)
Worked Example 2 (Technology – Active)
What are Complex Unfamiliar questions?
In QCAA Mathematics subjects, questions are split by degree of difficulty into Simple Familiar, Complex Familiar and Complex Unfamiliar questions.
Generally, 60% of each exam will consist of Simple Familiar questions. 20% of questions will be Complex Familiar, and the other 20% will be Complex Unfamiliar.
As the name suggests, Complex Unfamiliar questions are both complex and unfamiliar. Essentially, this means the following:
- You will be required to apply your knowledge of multiple different concepts to solve each question
- The information required to solve the question will not be obvious in its wording
- The question will most likely be in a context that you haven’t come across before
- Interpretation, clarification, and analysis will be required to develop responses to the questions
How do you answer Complex Unfamiliar Questions?
The most obvious ways to recognise a Complex Unfamiliar question include its position in the exam paper (generally at the end), the number of marks allocated to it (usually 6 or more), and unclear information and/or instructions.
Once you’ve identified a question as Complex Unfamiliar, the following steps can be followed to solve it:
Step 1: Highlight relevant information
Read through the question carefully once. Then, read it again whilst underlining/highlighting the key words or phrases.
This can include equations, units, variables and their definitions, what the question is asking you to do/find, and any other relevant information. If there are any tables or graphs, identify what these are trying to convey.
Step 2: Brainstorm concepts and formulas that may apply
Using this underlined/highlighted information, start brainstorming possible concepts, formulas, or techniques that could be applied to answer the question (e.g., sine rule, area between two curves, normal distribution etc.).
Think about similar questions you may have done in the past (if any) and what techniques you used to solve them.
If the question is technology active, think about where a calculator might be useful/necessary. Drawing a diagram or annotating an existing one might also help break things down!
Step 3: Identify your plan of attack
Use these ideas to come up with a general plan of attack. It’s also a good idea to come up with a backup plan, just in case your first idea doesn’t work out.
Sometimes it can be hard to envision any further than the first or second step. In this case, start with whatever you think should be done first and reassess from there.
The start of Year 11 can be overwhelming – this one reason is why!
Step 4: Progress through your solution
If things seem to be heading in the right direction, great! Keep going at it.
If you’re finding that your numbers are getting pretty wild, or that what you’ve found is totally unrelated to the question, that’s okay.
Go back and try to identify where you might have gone wrong or try a different approach.
Step 5: Make sure you’ve answered everything
It may take a few attempts to finally solve the problem, but it will be so satisfying once you get there.
Once you’ve solved it, go back over the question as well as your answer to ensure that you’ve answered everything. If possible, use your calculator or a different method to verify your answer.
Struggling to get through your Maths Methods exams? Here’s how to know if you should drop from Methods to General Maths for your QCE or not.
How do you prepare for Complex Unfamiliar Questions in your exam?
Despite the point of Complex Unfamiliar questions being that you mostly likely haven’t encountered them before, there are still many ways to prepare for when they pop up in your exams:
- Make sure you really understand the fundamentals of each concept. Identifying when to use what formulas/techniques can be the trickiest part of Complex Unfamiliar questions. Therefore, having a really strong understanding of how each concept is applied is essential.
- Complete a variety of practice questions, including as many Complex Unfamiliar questions as you can find. Although this doesn’t guarantee you’ll get the same questions in your exam, it definitely increases the likelihood of it and can help you develop the skills and strategies required to answer Complex Unfamiliar questions.
Extra Tips for Tackling Complex Unfamiliar Questions
- Leaving the Complex Unfamiliar questions till the end can be a good idea during the exams. This is because your brain will be ‘warmed up’ and ready to tackle more complex problems by the time you’ve completed the Simple Familiar and Complex Familiar questions. The only thing to keep in mind with this strategy is to ensure you leave enough time (30 – 40% of the allocated exam time) to do the Complex Unfamiliar questions.
- When completing questions, ensure that all of your working out is written out in a clear, logical manner. This is a good habit to get into, as in the exams, the number of marks allocated to each question is distributed across a number of different steps in the solving process, not just the answer.
In need of a Maths tutor in the Gold Coast? Learn about our holistic tutoring here!
Worked Example 1 (Technology – Free)
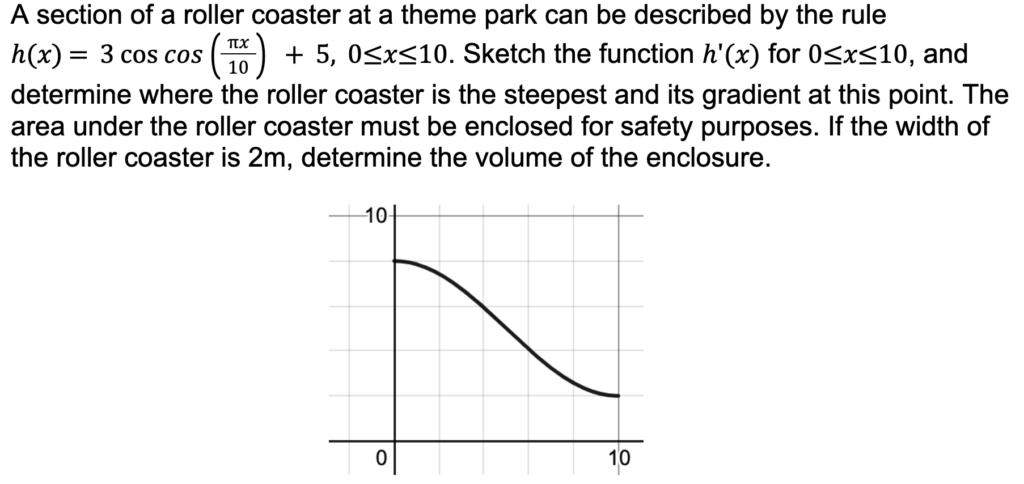
Question:
Step 1: Once I’ve read through the question, I would go back and highlight the information I think is relevant:
Step 2: From the highlighted information, it is clear that there are two parts to this question.
The first is about finding and sketching h'(x), as well as where the steepest point (i.e., the maximum) is and the gradient at this point. In order to find h'(x), differentiation would be the obvious method.
To find the steepest point, I would use the second derivative. The second part is about finding the area under the curve and using that to calculate the volume of the enclosure.
Because this is a Technology-Free question, we’ve been given a graphical representation of the curve to help us out. The term ‘area under the curve’ immediately suggests that integration will be used at some point.
Step 3: As I’ve got a general plan, I’d go ahead and get started by differentiating h(x) using the appropriate differentiation rules.
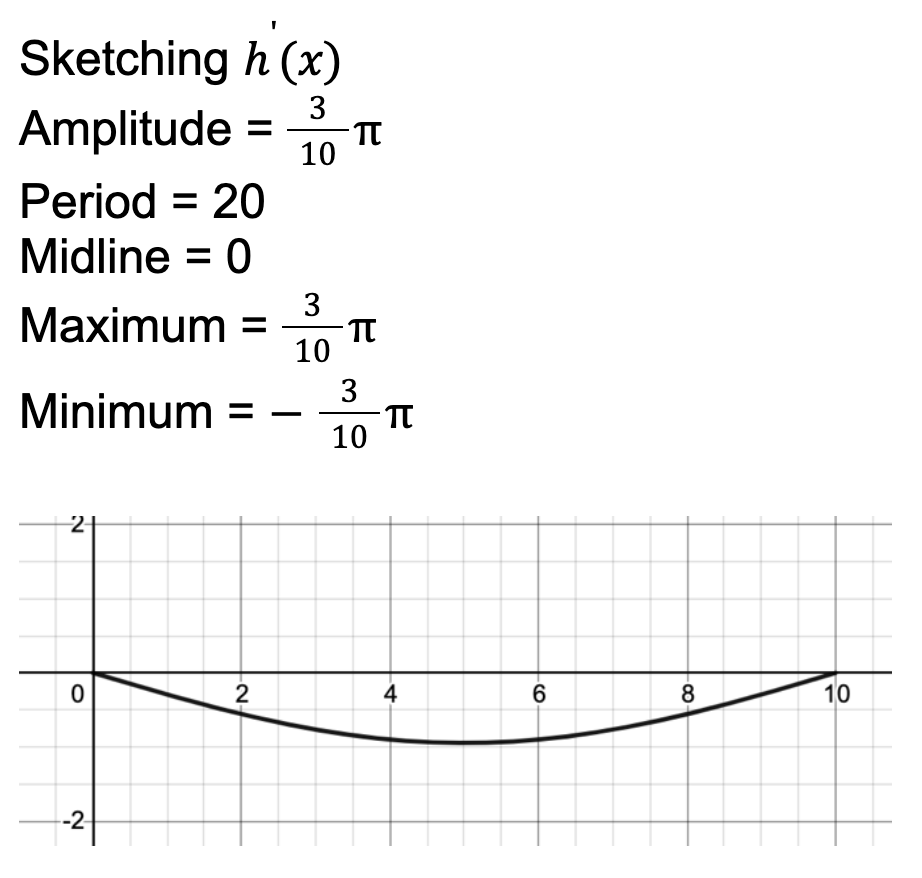
Now that we’ve found a function for h'(x), it’s time to sketch it. Firstly, I’d identify all the features.
Now it’s time to find where the roller coaster is the highest (within our given domain). It’s pretty obvious from the graph that it’s at (0,8), but we want to use mathematical procedures to confirm it.
The only two options that fit within our given domain are 0 and 10. To test which of these is a maximum point and minimum point, we need to find h”(x) and substitute in the x-values.
Finding nature of max/min points:
Now that we know the x-value of the steepest point, let’s substitute it back into the original formula to find the y-value.
Therefore, the steepest point of the roller coaster is at (0,8).
Step 4: We’ve solved the first part of the question! Now we can move onto the second part.
To find the area under a curve, we have to integrate the curve function between whatever domain we’re given.
Finding area under curve:
Now that we’ve found the area under the curve, all that’s left to do is calculate the volume.
Volume of enclosed region = 50 x 2 = 100 units3
Therefore, the volume of the enclosed region is 100 units3.
Step 5: Because we can’t use a calculator to double check our calculations at the end, I would try to be as accurate as possible. Nevertheless, it doesn’t hurt to go back and check your calculations.
Another thing you can do is to assess the reasonableness of your answers by asking yourself if your answers ‘seem right’. With this question, I would think to myself whether 50units2 sounds reasonable as the area of the region under the curve.
Worked Example 2 (Technology – Active)
Question:
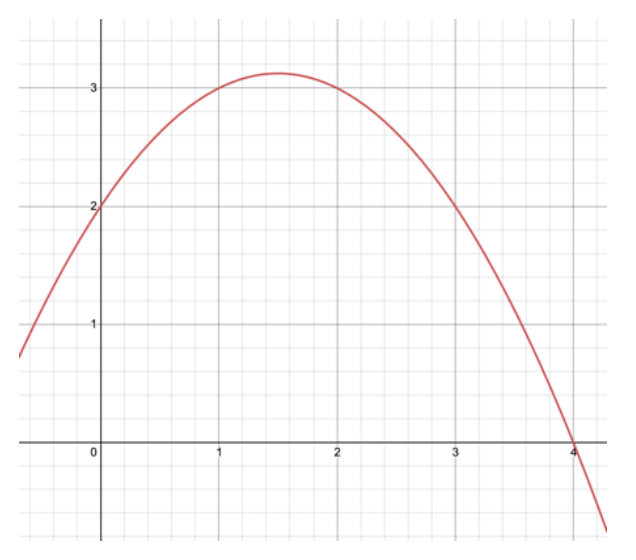
Determine the equation of the line y = mx + c that divides the area under the curve y = 0.5x(– x + 3) + 2 over [0, 4] into two equal regions. Justify all procedures using mathematical reasoning and evaluate the reasonableness of your answer.
Step 1: Once I’ve read through the question, I would go back and highlight the information I think is relevant:
Step 2: The term ‘area under the curve’ immediately suggests that integration will be used at some point. As we’re tasked with finding a linear equation, I know it is going to be a straight line that will divide the area under the curve.
The form of the curve itself will be parabolic, which I can tell from its equation (i.e., if you expand it, it becomes y=-0.5x2+1.5x+2).
As this is a technology-active question, I would also start thinking about how I could use my calculator to help me (possibly with evaluating the reasonableness of the answers). I would also note that we’re asked to justify all procedures.
Step 3: At this point, the first step of my plan would be to sketch the curve. The easiest way to do this would be to graph it on my calculator first, note the features such as intercepts and min/max points, and recreate it on the exam paper.
This way I have a rough idea of what the curve looks like, and what the equation of the line might look like.
My next step would be to use integration to find the area under the curve over [0, 4]. I would then divide this by 2 to find half the area under the curve.
This calculation is simple enough to do without a calculator, but if you’re short on time, then the calculator might be the way to go. The most effective method would be to work it out by hand and then verify using the calculator.
At this point, I’d start looking for ways to use the area value to find the equation of the line. Although the equation is given as y = mx + c, to simplify things, I would set the y-intercept to 0, making the equation y = mx.
The next assumption I would make is that the equation of the curve and the equation of the line intersect at a point x = a.
Step 4: So far, everything seems to be on the right track, so I’ll continue by using integration.
Just like the integration calculation before, it would be best to try to work this out by hand. Make sure to write out all your working out, and once you get an answer, double check on your calculator to confirm.
Step 5: Finally, I’d double check my answer by finding the area between the curve and the line using the integration function on my calculator.
On the hunt for other QCAA Maths resources?
Check out some of our other articles and guides below:
- How to Structure Your PSMT Report for QCAA Mathematical Methods
- The Ultimate Guide to Writing a Problem-Solving and Modelling Task (PSMT) Report for General Maths
- How to Ace Your External Assessment for QCAA Maths Methods
- How to Ace Your External Assessment for General Maths
- Should You Drop Down from Maths Methods to General Maths for the QCAA?
- How to Write Notes Using the QCAA Syllabus for Maths
Are you looking for some extra help with working through Complex Unfamiliar questions?
We have an incredible team of QLD tutors and mentors!
We can help you master the Maths syllabus and ace your upcoming Maths assessments with personalised lessons conducted one-on-one in your home or online!
If you’re looking for a Maths tutor in Brisbane, check out more info about our holistic tutoring here!
We’ve supported over 8,000 students over the last 11 years, and on average our students score mark improvements of over 20%!
We are also local to the Gold Coast, to support you with your maths needs!
To find out more and get started with an inspirational QLD tutor and mentor, get in touch today or give us a ring on 1300 267 888!
Yalindi Binduhewa is an Art of Smart tutor based in Queensland and was part of the very first cohort to go through the ATAR system, so she knows exactly how fun and enjoyable it can be. She is currently studying a Bachelor of Medical Imaging (Honours) at QUT and is loving it. When she’s not doing uni-related stuff or tutoring, she’s hanging out with her friends, rewatching a show for the 100th time, or trying out new crafty projects and discovering that she doesn’t have a talent for everything.