Studying Unit 4 for QCAA General Maths in class but feeling a little confused about what you need to know?
To make it easier for you, we’ve put together all the different topics you’ll be studying in this unit in this simple guide so that you can keep up with the content.
What are you waiting for? Let’s get into it!
What is Unit 4 in QCAA General Maths all about?
Topic 1: Compound Interest Loans and Investment
Topic 2: Reducing Balance Loans
Topic 3: Annuities and Perpetuities
Topic 4: Graphs and Networks
Topic 5: Connector Graphs and Flow Problems
Topic 6: Project Planning and Scheduling
Studying Methods instead? Check out how to ace Unit 4 of Maths Methods!
What is Unit 4 in QCAA General Maths all about?
Unit 4 in QCAA General Maths is perhaps the most difficult to learn in terms of practice and memorisation. That is because it contains skills to do with personal finance, that are extremely useful and applied after your studies, but are the most complicated as they deal with compound interests and annuities.
Nevertheless, they are very much learnable — they are by no means at the same knowledge level as Maths Methods. This guide will take you through Unit 4 step by step.
Topic 1: Compound Interest Loans and Investment
In the first topic, you’ll be thrown straight into finance, which is a major theme of Unit 4. In this first unit, you will utilise your work on sequences in your previous unit, and apply them to the concept of recurrence relations (sequences able to map finance).
In these you’ll find new terms such as the Principal (the money you start with before any investment or withdrawal), the Interest and the Product (the total money after the operation). Thus, you’ll then get to model interest and withdrawal schedules with recurrence relations.
Then, you’ll delve deeper into the concept of loans and investments in relation to compound interest, meaning you’ll be introduced to problems where you are asked to figure out an amount to pay back or an investment profit using the compound interest recurrence relation.
A0 = principal, An+1 = An + I
Finally, you’ll be introduced to effective interest and annual rate of interest, which are the most common rates used in the real world. Topic 1 comes in especially handy when you’ll have to borrow money from the bank for either your first car, uni student loans, or your first apartment.
Key Concepts
- Sequences and recurrence relations
- Modelling simple and compound interest situations
with recurrence relations- Investigating compound interest loans and investments
- Effective annual rate of interest
- Solving problems involving compound interest
Topic 2: Reducing Balance Loans
The second topic is all about reducing balance loans. These are loans on which interest is applied to the loaned amount itself.
This means that as you pay more and more of your loan back, the interest on the loan reduces, because the amount of the loan reduces. You’ll thus pay back less and less interest as time goes on.
This topic is short and sweet. You’ll learn a recurrence relation to model reducing balance loans, as well as practise enough questions with them to get you in gear for the final part of the finance section of the unit.
Key Concepts
- A recursive model for reducing-balance loans
- Investigating reducing-balance loans
- Solving problems involving reducing-balance loans
Topic 3: Annuities and Perpetuities
Annuities and Perpetuities are the last finance-related concepts you’ll be studying in General Maths. This topic is extremely useful, as annuities are something you definitely want to consider in terms of investment.
Annuities are nothing more than money invested by you, that over time is paid back to you with interest. In other words, the society or company that benefits from your initial investment pays you back your own money as well as interest, given, of course, that company’s success.
You’ll learn a recurrence relation for these too, and you’ll be asked to solve problems in relation to annuities. Most of these will involve figuring out monthly payments, the initial principal, or even the interest rate. All this requires is the rearrangement of the formula.
Seeing as there are a few formulas and recurrence relations to memorise, make sure you spend some time doing these in the exam. Practise these as much as possible in varying levels of difficulty.
The revision chapters and the chapter questions in your textbook, as well as past exam papers, are all a great way to make sure this knowledge you have is solid on the topic. An example of an annuity is shown below:
A0 = 5000, An+1 = 1.01 × An – 1030
Lastly, you’ll be introduced to perpetuities. These are much simpler compared to annuities, as they are paid back at a constant rate. Meaning if you put $170,000 in a monthly perpetuity, you’ll be paid at the same rate monthly, regardless of interest.
Key Concepts
- Recursive model for annuities
- Investigating annuities
- Solving problems involving annuities with technology
- Perpetuities
Deciding between public vs private ATAR schools? Check out our list of the top schools in Brisbane here!
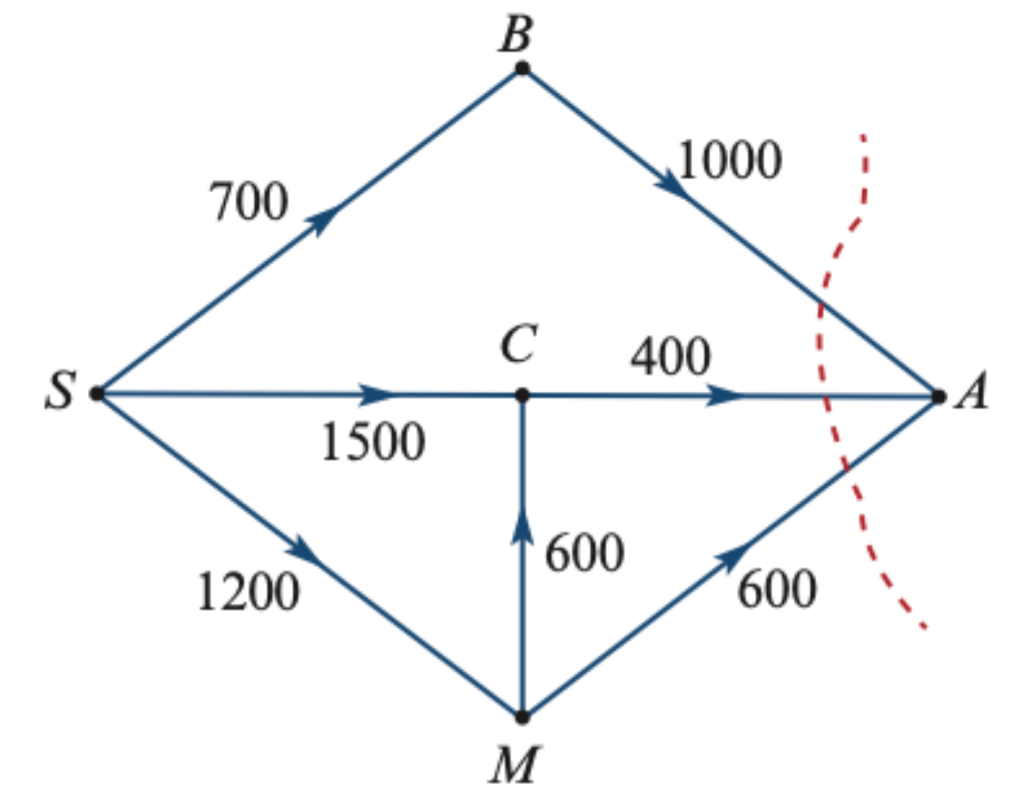
Topic 4: Graphs and Networks
This topic is about concepts that you’ll have probably never encountered before. Ever wondered how CEO’s delegate tasks or plan a project out in steps? They do this through graphs and networks, but not the kind we’ve been use to so far.
But first, this topic will give you a general idea on how to navigate such graphs before you get to apply these skills in later topics.
You’ll be introduced to terminology, such as a ‘walk’, ‘path’ and ‘cycle’, as well as different types of graphs, like planar, Eulerian and Hamiltonian. The great thing about this topic is that it’s very visual, so a lot can be discerned by just looking.
The purpose of such graphs is mainly to understand how long a particular activity or project would take. Hence, as your last concept, you’ll tackle the idea of the shortest path.
Meaning, in a weighted graph (where every step has a number as weight) what is the path with the lowest amount of combined weight?
Image sourced from Cambridge Senior Mathematics for Queensland, General Mathematics
Key Concepts
- Graphs and associated terminology
- The adjacency matrix
- Planar graphs and Euler’s formula
- Exploring a graph
- Eulerian graphs and applications
- Hamiltonian graphs and applications
- Weighted graphs, networks and shortest path problems
Topic 5: Connector Graphs and Flow Problems
The fifth topic builds on what you learned in the previous chapter, only it puts graphs in a different perspective.
Here, you’ll learn about Flow, and features such as Cuts and Dummies. These are simply ways to indicate an interruption, or possible interruption of flow from the start to the finish of the graphs.
This system is widely used to represent pipelines and other problems with flow as their main feature.
Also studying Unit 4 of QCE Physics? Check out our Ultimate Guide on that too!
You’ll be introduced to tree and connector problems which are somewhat unrelated to Mathematics, but are nice visual puzzles.
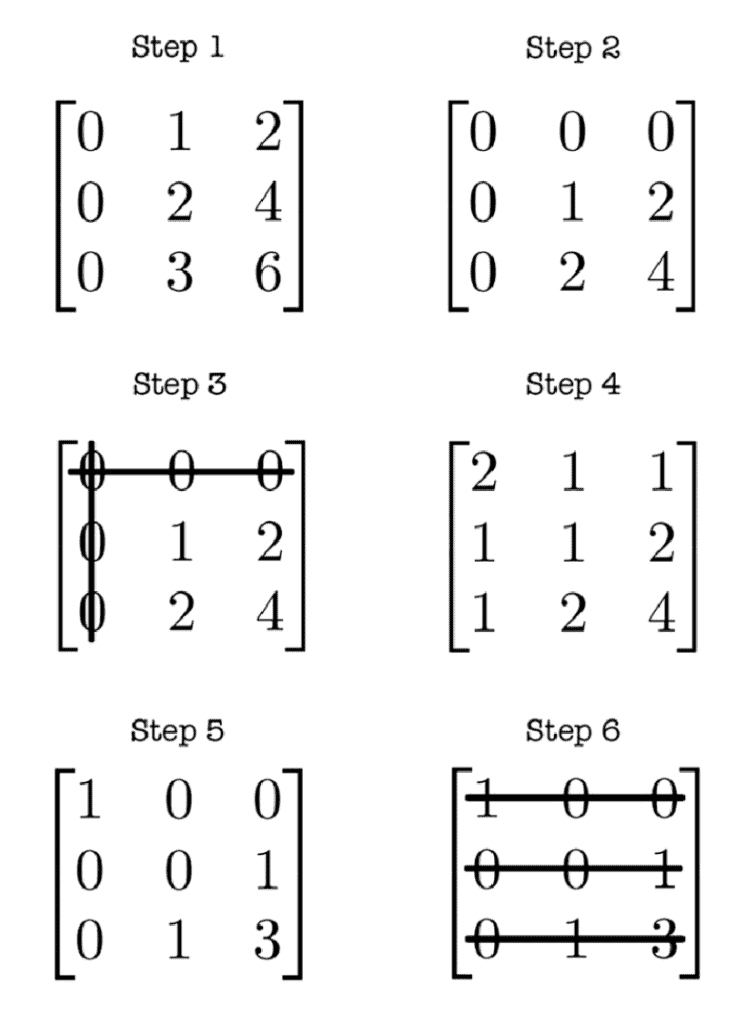
The most difficult part of this topic are to do with the Hungarian Algorithm. This is, in short, a system arranged in matrix format to determine the lowest cost of a particular variable, from employee salaries to number of hours.
Students tend to find this process challenging because there are a few steps to remember, and these often result in a mix up. A way to avoid this is just practise and practise as much as you can.
Key Concepts
- Factor Trees and connector problems
- Assignment problems and the Hungarian algorithm
- Flow networks
Topic 6: Project Planning and Scheduling
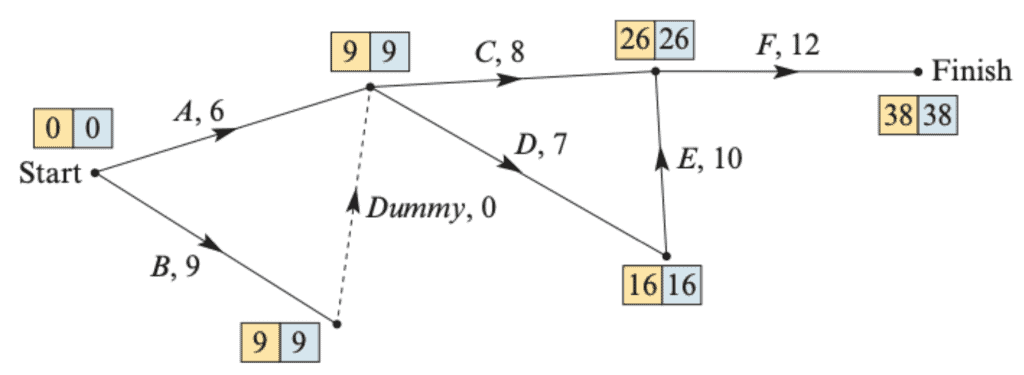
In the last topic, you’ll be introduced to project planning using graphs. You’ll have to think graphs as representing the beginning and end of a project, rather than just a sequence of actions. Nevertheless, all this is pretty straight forward.
You’ll then be introduced to terms such as Latest Finishing Time, and Earliest Start Time. These refer to the project, and are useful to execute forwards and backwards scanning to find the Critical Path (the best path to complete the project).
This is another concept you’ll have to practise — here’s an example:
Image sourced from Cambridge Senior Mathematics for Queensland, General Mathematics
Lastly, you’ll be applying your newfound knowledge to problems.
Key Concepts
- Project planning – precedence tables and activity networks
- Scheduling problems
- Applications of critical path analysis
On the hunt for other QCAA General Maths resources?
Check out our other articles and resources below:
- Download QCAA General Maths Practice Exam for External Assessment Revision
- How to Ace Your External Assessment for General Maths
- QCAA Multiple Choice Practice Questions for Unit 3 & 4 General Maths External Assessment
Also studying Chemistry? Chances are you’re stuck on organic chem… we get it!
Are you looking for some extra help with revising for QCAA General Maths Unit 4?
We have an incredible team of QLD tutors and mentors!
We can help you master the QCAA General Maths syllabus and ace your upcoming General Maths assessments with personalised lessons conducted one-on-one in your home or online!
Looking for Maths tutoring in the Gold Coast? Learn more about our holistic Maths tutoring here!
We’ve supported over 8,000 students over the last 11 years, and on average our students score mark improvements of over 20%!
To find out more and get started with an inspirational QLD tutor and mentor, get in touch today or give us a ring on 1300 267 888!
Vittorio Manessi is an Art of Smart tutor based in Queensland studying environmental science. He was one of the first Year 12 students to study under the new ATAR system in Queensland. He enjoys Maths, Science, English and Ancient History and is keen to share his knowledge of the QCE by making awesome resources.