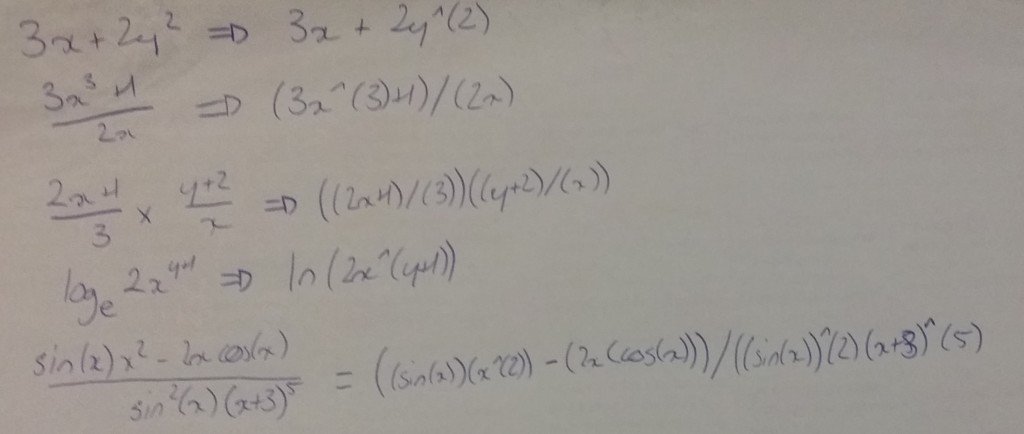Let’s be honest here – no one has the time to hunt down millions of practice questions. This goes double for situations where you’re looking for that one highly specific type to really double down on something you’re not 100% comfortable with. The solution here is surprisingly simple – just make your own!
Wait, what? How does one even? Fret not – it’s actually pretty easy. You may or may not have heard of Wolfram Alpha, the computational knowledge engine.
What is Wolfram Alpha?
In short, it’s like Google for numbers – you can use it to solve equations, perform complicated calculus and about 3.7 billion other things AND it gives you full worked solutions if you’re willing to spend a bit of cash to go Pro!
First, you’ll need a quick tutorial on how to use it – it’s really very easy, but figuring it out on your own can be painful.
This is probably a good time to mention Wolfram Alpha isn’t your only option – other programs like Mathematica (which is also written by Wolfram) can do much the same things.
Wolfram Alpha has certain benefits that make it better for our purposes – for one, it’s free, which is nice. It’s also online, and much more user friendly. The big kicker is that it provides worked solutions, though, although that does come at a cost. So if you have a program that you’re familiar with, you can try and use it instead, but Wolfram Alpha is probably better built for these purposes.
If you’re planning on taking up anything Maths based at University (i.e. Commerce, Chemistry, Pure Mathematics), you might want to consider purchasing it. A nerdy birthday present if you will! Combine help from Wolfram Alpha and personalised feedback from our HSC Maths Tutors Sydney to get the ultimate form of accelerated learning!
The Basics: Computational Formatting – The Language of Wolfram
It doesn’t take a genius to recognise that your keyboard isn’t built to type maths formulae as they’re written in textbooks. That kind of presentation is called standard or professional formatting.
For computers, they need the equations written in what’s called computational or digital formatting.
You’re probably already familiar with the most basic conventions, especially if you’ve ever worked with Excel – but for this tutorial, we’ll assume you know nothing and work from the ground up. So, when you’re entering your equations into Wolfram:
- + operates as plus, and – as minus (as well as a negative sign). The equals sign (=) also works just like normal. These ones aren’t too shocking, I hope. So, for example, 3+5=8 and 2-3=-1.
- Multiply using * (shift+8). So, say, 2*4=8. You can leave this out in all the same ways you can leave out a multiply sign in algebra – so 3*x and 3x are read as the same thing.
- Divide using /. This is also used for fractions. So, for example, 4/2=2, and a quarter is written as 1/4.
- For indices/powers, use ^ (shift+6). So, per se, 2 cubed looks like 2^3.
- It’s a good idea to put brackets around whatever is in the exponent position, no matter how simple, to keep Wolfram from getting confused. So, write 2 cubed as 2^(3), or x to the power of 2y+1 as x^(2y+1).
- For trig functions, just type them as plain text. For log functions, entering “log” will return log base 10 – use ln for base e. Enter the argument (so, the thing the function is operating on) in brackets. So, calculating the sine of 3x+2 would look like sin(3x+4).
- Important constants – for π, just type “pi” like it was number. Same goes for e.
- Overdose on brackets. Wolfram can’t handle as much ambiguity as a human eye can, so unless your equation is 100% accurate, Wolfram will either return the wrong answer or no answer at all. For that reason, we abuse brackets to make our formulae super clear. Using four or five sets of brackets in a single term isn’t too uncommon in digital formatting.
- While you’re still a fledgling with this stuff, it’s a good idea to put every term and every exponent in it’s own set of brackets. More brackets is safer than less!
Here a few examples to help familiarise yourself with the concepts. Try just writing random flows of algebra and then converting it yourself – practice makes perfect!
Another good way to practice your digital formatting is the equation tool in Microsoft Word.
- If you’re running Windows, press alt+= to activate it, or on a Mac it’s in the ribbon under Document Elements.
- Type in your target equation in digital formatting, and Word will automatically change it into professional formatting.
- If it looks right, you’ve entered it right!
Conversely, you can enter the equation manually, using “equation tools” in the ribbon and then right-click on the finished equation. Select “Linear”, and the equation will change into digital format, letting you read off the correct answer.
So now you can give Wolfram an equation – but how do you tell it what to do with it?
Those are called commands, and they’re inconsistent between different pieces of software – what works in Wolfram Alpha doesn’t always work in Mathematica, and so on.
So this section will only help you work Wolfram – you may need to relearn these if you switch software in future. Most of these commands are fairly simple, so they shouldn’t be too hard to learn.
- If you want Wolfram to solve an equation (that is, return an x-value), just enter “solve (equation) for (variable)”. So, to solve 13x^3+3x^2+2=15, enter “solve 13x^3+3x^2+2=15 for x”.
- For derivatives (which you may also see called differentials), enter “derivative of (function) with respect to (variable)”. So, to instead differentiate the function from the last example, we’d use “derivative of 13x^3+3x^2+2 with respect to x”.
- For indefinite integrals, just replace “derivative” by “integral” – so “integral of 13x^3+3x^2+2 with respect to x”. For definite integrals, add “between (lower limits) and (upper limit)” to the end. So, using -1 and 1 as limits, the command becomes “integral of 13x^3+3x^2+2 with respect to x from -1 to 1”.
- If you want a graph of f(x), simply enter “y=f(x)”, or “plot f(x)”. So, for our example function, either “plot 13x^3+3x^2+2” or “y=13x^3+3x^2+2” will return a nice graph.
That should just about cover everything you need to know about using Wolfram at your level. If you’re finding you’re looking for more, then Wolfram does have an inbuilt instruction manual. Just click on the “mathematics” tab under the search bar, and it should cover you.
So now you’re a low key professional at Wolfram Alpha, but what is that actually good for? Among some other stuff, making practice questions of course! There are two ways you can do this – you can modify a known question and use Wolfram to provide a solution, or you can build it from the ground up!
Question Type 1 – Modifying Knowns
I’m pretty sure you can see where this is going already. All you have to do is find some old question from some old exam, change up the numbers, and then get Wolfram to do the heavy lifting for you. So, let’s say you’ve hunted down this question:
2014 2U HSC 16(b): At the start of a month, Jo opens a bank account and makes a deposit of $500. At the start of each subsequent month, Jo makes a deposit which is 1% more than the previous deposit. At the end of every month, the bank pays interest of 0.3% (per month) on the balance of the account.
First, just do the question! It’s silly to find a practice question and then not use it. After you’ve done the question and checked your answer, try it again with different numbers. Perhaps you think having $500 isn’t a realistic starting point, so you decide to drop it to $200, and perhaps you’re crushingly aware 0.3% interest per month is very very high, so you decide to reduce it 0.18%. From the solutions that were provided with the paper, we know that the equation everything boiled down to was this:
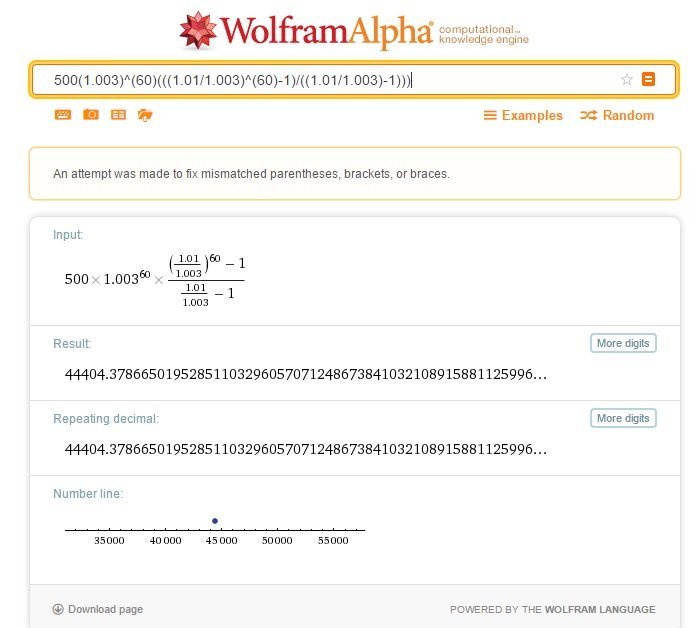
And then given our substitutions, some of those values will change. So our fundamental equation will be a bit different. In digital formatting, it’s 500(1.003)^(60)(((1.01/1.003)^(60)-1)/((1.01/1.003)-1))). So we pop that into Wolfram.
And voila! It’s worth noting that sometimes, it’s worth just entering the question into the search bar like you were Googling it (remember, that means distilling it down to key words, not copy-paste) – Wolfram is really really clever, and sometimes it can give you an answer with just that.
Okay so I lied a little bit. It doesn’t give you an answer straight up, but that little bit at the bottom there is a calculator built to do exactly the thing you just asked! Pretty neat, huh?
It’s also worth noting for this question, the changes were computational, so we don’t need a worked solution – basically we just used Wolfram as a high-tech calculator. I’ll show you how the solutions work in the next section!
Question Type 2 – Make it from Scratch!
Now this here is the fun part. You have two choices – make a pure maths question, or an applied maths question. By pure maths, I mean something that’s contextless, like a trigonometric identity or a relationship between roots and coefficients. To be frank, there’s not much point doing these until you’re at 4 Unit level, and even then scarcely.
Pure maths questions in the HSC are designed to tick boxes, and check you can do the maths.
The discriminating questions are the applied ones where you actually have to think about how the maths works and why that makes it useful (yes, maths is useful. I was surprised too).
For the 4U students, it’s probably not worth your while trying to use Wolfram to make pure maths questions.
If you’re at the level where you’re even capable of coming up with a line you can follow for questions of that complexity, you’re well above the level where you need more practice questions, so you can satiate yourself with past papers. There are plenty of fun applications of 4U content (especially complex numbers) that you can explore, so if you’re developing new questions, pick your battles wisely and stick to applications. Conversely, stick to more simple questions that you can easily check yourself.
So, now for the fun stuff.
I bet you didn’t know all the things you’ve learned in maths class run deeply through all sorts of real life fields. Science, finance and statistics (which quite literally underpins everything) are all based on the things you’ve learned in maths class. So try and fire up your brain and find some fun applications for what you’re doing! A good starting point are those tabs underneath the search bar on the Wolfram homepage. They’re pretty instructive as far as fields you can research. Now, I’m a chemist-in-training, so I’m going to go straight to Chemistry.
Step 1: Creating a Concept
First, you need a concept for the question. Try using Wolfram like Google. Search something like “integration in chemistry” and see what happens. Chances are, not a lot.
Wolfram’s algorithms are very focused, so it’ll pick out the “integration” part of that sentence and try to find a function in there to integrate – and when it can’t it’ll get mad and sulk without ever giving you an answer. A good approach then is to just Google it with normal Google.
In about 10 seconds, I’ve found out integration is used in chemistry to model reaction rates. Great! I have a concept now.
Step 2: Finding a Model
Now, research that concept in a bit more depth, with focus on the mathematical model that underpins it. You’ll find all sorts of stuff – if you’ve gone down a science line, Khan Academy is brilliant (and they also have a growing finance section), and there are lots of podcasts and YouTube channels that are fantastically informative in all sorts of fields.
What you’ll find is there’s maths – at some level, there is an equation you can solve, or a value you can calculate. For our example of reaction rates, integration is used to determine how much of a given chemical I have at a given time. With this information, write a short preamble for the question that explains how the maths is used. For our example question;
“In chemistry, it’s common practice to plot concentration of certain reactants against the reaction time. This produces a graph with slope -dC/dt, where C is concentration in mol/L and t is time in minutes. Because reactions can be plotted on predictable graphs based on a variable called their reaction order, integrating dC/dt gives us an easy way to predict the yield at any given time – a function C(t).”
To read, that might seem like something out of a Chem exam – but look at all the maths in there! There’s a derivative, and a full Cartesian graph for C(t). Think of this the same way you would a question about natural growth – there’s nothing mathematical about a bunch of rabbits breeding on an island, but you still get questions about that, because we can use maths to model the behaviour of the population over time.
Step 3: Asking the Question
So now we have a concept and a model – time to figure out what we can ask! Obviously, this one is about calculus. So from there, are we integrating? Differentiating? What’s going on?
This question is about integrating, so let’s ask them to integrate! We also know uses of definite integral in the model from our research, so we can ask about them, too. Since this is similar to natural growth, try modelling the question after a natural growth question.
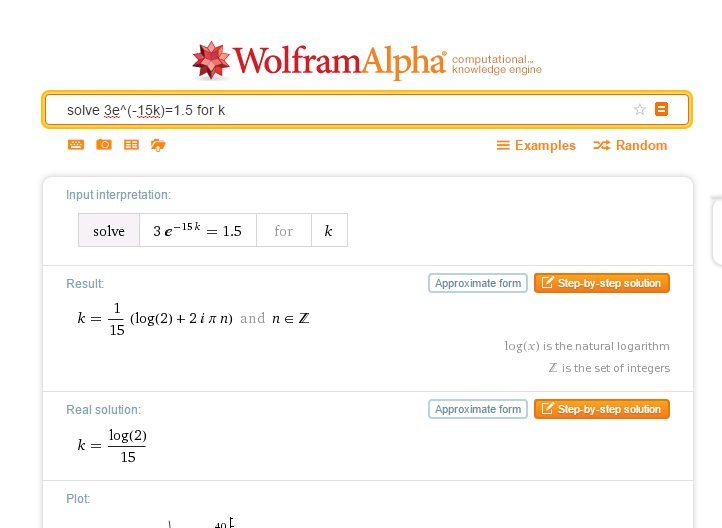
(a) Given a certain reaction obeys -dC/dt=kC for some real constant k, find C(t) provided the concentration at t=0 is 3 mol/L.
(b) If the concentration after 15 minutes is 1.5 mol/L, find a value for k.
See how, even though it may not seem directly relevant to maths, you can take a certain angle to make it relevant? That’s the idea here! HSC questions are purpose-built to distract you from the maths with needless language – writing that language in will help you understand why it’s there, and why you can ignore it.
So now, what does Wolfram have to do with all of this? Well, you have to get your answers from somewhere, don’t you? I’m not saying we don’t trust you to calculate the answers yourself, I’m just saying if we can get a perfect solution from a computer, why not?
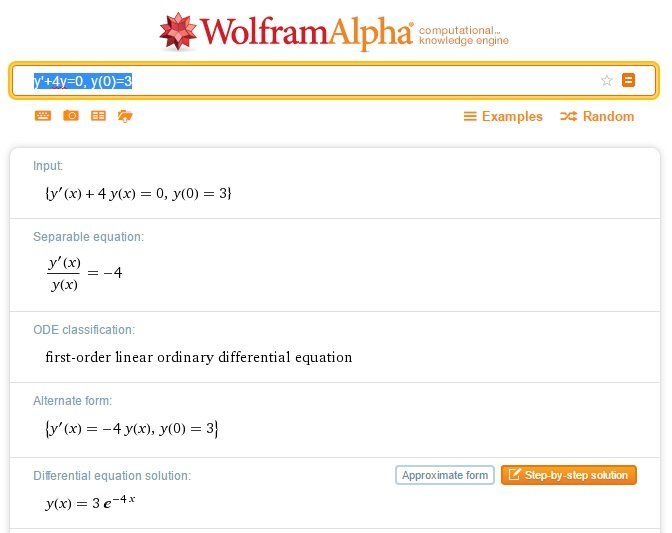
So, for part (a), we have a differential equation – in fact, it is natural decay! So, what we do is this:
Now, I know I didn’t explain how to enter differential equations. But if you enter “solve differential equations” into the search bar, Wolfram will teach you. Also, it doesn’t like have undefined constants (i.e. k) in there, so the fastest way is to substitute some real number for k, and then swap k back in at the end. You’ll learn little odds and ends like this as you go – it’s all about practice.
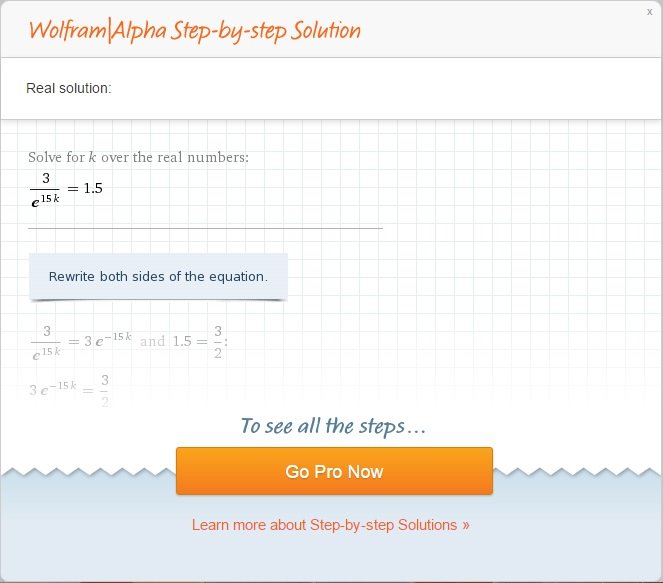
If you click “step-by-step solution”, Wolfram will prompt you to go pro. It’s not too expensive and the software is pretty powerful, so it’s worth considering if you need the guidance. You should be able to see the first few steps anyway if you sign up for a free account – that might give you the clue you need to crack the thing.
Part (b) is pretty simple algebra, but we’ll use Wolfram anyway. It’ll look a bit like this:
The”result” section has taken into account the possibility of k being a complex number – but the question (as well as common sense) tells us it’s real, so we can just read the “real solution” section.
For the step-by-step solution, you’ll be able to see this:
It’s not exactly a full solution, but it’s a head start.
So there you have it! It may seem a bit silly, but it’ll actually be extremely educational.
Seeing how question writing technique works will help you snipe for marks in exams and you’ll get to see maths in a new light – it’s not just a bunch of numbers, it’s a real thing with real uses! This reaction rates example is extremely important in the production of medicines and plastics as well as cooking. That’s right – that equation could be happening in your oven right now. Isn’t that cool?
Not to mention, writing your own practice questions and trading with friends can save you bucket loads of precious, precious time.
A few other interesting examples you can explore include the Gini Index for economic inequality or the Fourier transform, an extremely useful result in physics that’s used in everything from quantum mechanics to electronic music!
Be warned – the Fourier transform involves complex numbers, so it’s only suitable for 4U students. You can also research specialist applications – if you’re a foodie, explore molecular gastronomy. The concept of spherification (which is responsible for the bubbles in bubble tea, among other things) stands on the same model of reaction rates we used above, but with a slightly different setup. You can find more information here.
You can really let your creativity run wild here!
You’ll be surprised to see all the things maths can be used for – especially if you expand your range to include statistical models. You could explore the maths of colour, of cars, or of Charles Dickens – there’s a model suitable for all of them, I promise.
Think outside the square, and you’ll find you can stop thinking of maths as a formula sheet and more as a concept that can underpin other things – and that’s a breakthrough even third year university students often struggle to make.
Aiming for a Band 6 in Standard or Advanced Maths? Check out our article here for tips!
Looking for some extra help with HSC Maths?
We have an incredible team of HSC Maths tutors and mentors who are new HSC syllabus experts!
We can help you master the HSC Maths syllabus and ace your upcoming HSC assessments with personalised lessons conducted one-on-one in your home or at our state of the art campus in Hornsby!
HSC Math subjects are some of the most difficult! Don’t do it alone! Check out our local tutoring options, such as our HSC Maths tutoring in Blacktown and Sutherland Shire!
We’ve supported over 5,000 students over the last 10 years, and on average our students score mark improvements of over 19%!
To find out more and get started with an inspirational HSC English tutor and mentor, get in touch today or give us a ring on 1300 267 888!
Matt Saunders is a huge nerd who first got into writing through fanfiction. He’d known science was the path for him since a young age, and after discovering a particular love of bad chemistry jokes (and chemistry too), he’s gone onto to study Forensic Chemistry at UTS. His HSC in 2014 was defined in equal parts by schoolwork and stagecraft, which left him, weirdly enough, with a love of Maths strong enough to inspire him to tutor any level, along with 7-10 Science and HSC Chemistry.